Orbital mechanics and design

V. Hunter Adams (vha3), MAE 4160/5160, Spring 2020

from IPython.display import Latex
from IPython.display import Image
from IPython.core.display import HTML

In this document:

1. Review of Keplerian motion
2. Review of ellipse geometry and orbital parameters
3. Kepler's Laws (discussion and derivation)
4. Orbital perturbations
5. Geostationary orbits
6. Molniya orbits (frozen orbits and repeat ground tracks)
7. SSO orbits
8. Introduction to constellations
9. GPS constellatin
10. Iridium constellation
11. Starlink

This lecture is about the orbits into which we place spacecraft. The next lecture is about how we get the spacecraft to those orbits.

Other Reading

1. SMAD 9
2. SMAD 10

Orbit Mechanics Review

Keplerian motion

We'll start by considering the two-body problem. This problem considers the interaction between two point masses that are only acted upon by the gravitational force (no perturbations), as shown below.

Image(filename = "bodies.png", width=600, height=600)

$\textbf{r}$ is the vector separating $M$ and $m$ (points from $M$ to $m$). The unit vector that points in the direction of $\textbf{r}$ is $\hat{\textbf{r}}$. The forces acting on each body are given below:

\begin{align} \textbf{F}_m &= -G \frac{M m}{||\textbf{r}||^2} \hat{\textbf{r}}\\ \textbf{F}_M &= G \frac{M m}{||\textbf{r}||^2} \hat{\textbf{r}} \end{align}

Where $G$ is Newton's Gravitational Constant. In order to find the equation of motion for $m$, we apply Newton's second law:

\begin{align} m \ddot{\textbf{r}} &= -G \frac{Mm}{||\textbf{r}||^2} \hat{\textbf{r}} \end{align}

Simplifying:

\begin{align} \boxed{\ddot{\textbf{r}} = -G \frac{M}{||\textbf{r}||^2} \hat{\textbf{r}}} \end{align}

We often see this equation written in terms of $\mu = GM$:

\begin{align} \ddot{\textbf{r}} = -\frac{\mu}{||\textbf{r}||^2} \hat{\textbf{r}} \end{align}

This equation describes planar motion, which is characterized by Kepler's Laws. We'll discuss those momentarily. Before doing so, I'd like to make an observation. Through the notation used above, we've implied that one of the masses, $M$, is significantly larger than the other mass, $m$. One represents a planet, the other a spacecraft. We can define a polar coordinate system with its origin at the center of mass of the more massive body, $M$, and parametrize the vector $\textbf{r}$ in terms of those polar coordinates, as shown below:

\begin{align} \textbf{r} &= \rho \hat{\rho} + \theta \hat{\theta} \end{align}

Where $\rho$ is the distance separating the two bodies, and $\theta$ is the polar angle that rotates that magnitude vector to the position of the mass (true anomaly). The above equation of motion for the vector $\textbf{r}$ can be separated into an equation of motion for the radial component $\rho$ and the angular component $\theta$ as shown below:

\begin{align} \boxed{\ddot{\rho}= -\frac{G M}{\rho ^2} + \rho\dot{\theta}^2} \end{align}

\begin{align} \boxed{\ddot{\theta} = -\frac{2\dot{\theta}\dot{\rho}}{\rho}} \end{align}

These equations are useful for discussing Kepler's Laws.

Kepler's First Law

Discussion

Kepler's first law states that orbits are conic sections (circles, ellipses, parabolas, and hyperbolas). The solution to the above two-body problem is given below. Any conic section can be a solution to this equation.

\begin{align} \rho(\theta) &= \frac{a(1-e^2)}{1+e\cos{\theta}}\\ \end{align}

Where $a$ is the semimajor axis, $e$ is the eccentricity, and $\theta$ is the true anomaly. It's worth pausing for a moment to review some ellipse geometry and orbital mechanics vocabulary.

A brief aside on ellipse geometry

A labeled picture:

Image(filename = "ellipse.png", width=600, height=600)

Some definitions:

\begin{align} a&: \text{ semi-major axis}\\ b&: \text{ semi-minor axis}\\ e&: \text{ eccentricity}\\ \theta&: \text{ true anomaly}\\ \rho &: \text{ radial distance (polar coords)}\\ p&: \text{ semi-latus rectum}\\ c&: \text{ linear eccentricity}\\ r_a&: \text{ apoapsis distance}\\ r_p&: \text{ periapsis distance}\\ A&: \text{ area} \end{align}

Some useful relationships:

\begin{align} 1 &= \frac{x^2}{a^2} + \frac{y^2}{b^2}\\ A &= \pi a b\\ r_p &= a(1-e)\\ r_a &= a(1+e)\\ e &= \frac{c}{a} = \sqrt{1 - \frac{b^2}{a^2}} = \frac{r_p - r_a}{r_p + r_a}\\ p &= \frac{h^2}{\mu} = a(1-e^2)\\ \rho &= \frac{a(1-e^2)}{1+e\cos{\theta}} = \frac{r_p(1-e)}{1+e\cos{\theta}} = \frac{p}{1 + e\cos{\theta}} \end{align}

A reminder about orbital parameters

These are the six parameters that are used to uniquely specify an orbit. They divide into three categories: those which define the shape of the orbit, those which define the orientation of the orbit in inertial space, and those which define the location of the spacecraft on that orbit.

Size and shape of orbit: The following two orbital parameters define the size and shape of an orbit:

1. Semi-major axis, $a$
2. Eccentricity, $e$

Orientation of the orbit: The following three orbital parameters define the orientation of the orbit in space:

1. Inclination, $i$
2. Longitude of the ascending node, $\Omega$
3. Argument of periapsis, $\omega$

Location of satellite in orbit: The remaining parameter specifies the location of the spacecraft along the orbit.

1. True anomaly, $\theta$ ($\nu$ in the illustration below)

See the illustration below.

Image(filename = "params.png", width=600, height=600)

Derivation

(with help from http://farside.ph.utexas.edu/teaching/336k/Newtonhtml/node40.html#e6.46)

Consider the radial equation of motion for the spacecraft in the xy plane, provided above:

\begin{align} \ddot{\rho} - \rho\dot{\theta}^2= -\frac{G M}{\rho ^2} \end{align}

This can be rewritten in terms of the angular momentum, $h = m\rho\dot{\theta}$:

\begin{align} \ddot{\rho} - \frac{h^2}{m^2 \rho^3} &= -\frac{GM}{\rho^2} \end{align}

In the previous section, it was shown that $h$ is constant. Pulling a trick, make the following substitution:

\begin{align} \rho(\theta) &= u^{-1}(\theta) \end{align}

This implies the following:

\begin{align} \dot{\rho} &= -\frac{\dot{u}}{u^2}\\ &= -\rho^2(\theta)\frac{du}{d\theta}\frac{d\theta}{dt}\\ &= -\rho^2(\theta)\dot{\theta}\frac{du}{d\theta}\\ &= -h \frac{du}{d\theta} \end{align}

\begin{align} \ddot{\rho} &= -h \frac{d^2u}{d\theta^2}\frac{d\theta}{dt}\\ &= -h\dot{\theta}\frac{d^2u}{d\theta^2}\\ &= -u^2h^2\frac{d^2u}{d\theta^2} \end{align}

This allows the radial equation of motion to be rewritten in linear form:

\begin{align} \frac{d^2u}{d\theta^2} + u &= \frac{GM}{h^2} \end{align}

This differential equation has a general solution given by:

\begin{align} u(\theta) &= \frac{GM}{h^2}\left[1+e\cos{(\theta-\theta_0)}\right] \end{align}

for arbitrary constants $e$ and $\theta_0$. Without loss of generality, we can set $\theta_0$ to zero and solve for $\rho(\theta)$:

\begin{align} \rho(\theta) &= \frac{\rho_c}{1+e\cos{\theta}} \end{align}

where $\rho_c = \frac{h^2}{GM}$. This can be recognized as the equation for an ellipse. More commonly, $\rho_c$ is written in terms of the semimajor axis and eccentricity of the ellipse:

\begin{align} \rho(\theta) &= \frac{a(1-e^2)}{1+e\cos{\theta}} \end{align}

Kepler's Second Law

Discussion

Kepler's second law states that the line segment which joins a satellite and the central body sweeps equal areas in equal times. This is tied to the conservation of angular momentum, as shown below.

Derivation

Taking a step back, let us consider the angular momentum for the spacecraft, modeled as a point mass:

\begin{align} {\bf{h}} &= I\dot{\theta}\\ &= m\rho^2\dot{\theta} \end{align}

Multiply both sides of the equation for tangential motion (provided above) by $m\rho$:

\begin{align} m\rho^2\ddot{\theta} + 2m\rho\dot{\theta}\dot{\rho} = 0 \end{align}

The above equation could be rewritten as:

\begin{align} \frac{d}{dt}\left(m\rho^2\dot{\theta}\right) &= 0\\ \frac{d}{dt}{\bf{h}} &= 0\\ \end{align}

This shows that angular momentum is conserved under our dynamics assumptions. Consider the path that the spacecraft takes in a very short amount of time, shown below:

Image(filename = "kepler.png", width=600, height=600)

The area swept out by the spacecraft is approximately a triangle with height $\rho$ and base $\rho \partial{\theta}$. The area of this triangle is given by:

\begin{align} A &= \frac{1}{2}\rho^2\partial{\theta} \end{align}

The rate at which this area is swept out is given by:

\begin{align} \frac{dA}{dt} &= \frac{1}{2}\rho^2 \frac{d\theta}{dt}\\ &= \frac{1}{2}\rho^2 \dot{\theta}\\ &= \frac{{\bf{h}}}{2m} \end{align}

It has been shown that the angular momentum is constant, so the rate of area accumulation is also constant. The spacecraft sweeps out equal areas in equal times.

Kepler's Third Law

Discussion

Kepler's third law states that the square of the orbital period is proportional to the cube of the semi-major axis of the orbit. Specifically:

\begin{align} T^2 &= \frac{4\pi^2a^3}{GM} \end{align}

Derivation

It has been shown that the trajectory of a spacecraft under the dynamics assumptions traces out an ellipse, and that the spacecraft sweeps equal areas in equal times. This can be used to find the relationship between the semimajor axis of the ellipse and the orbital period of the spacecraft.

\begin{align} T &= \frac{A}{dA/dt} \end{align}

$A$ is the area of the ellipse, given by $\pi ab$. $dA/dt$ is, as shown above, $\frac{h}{2m}$. Thus:

\begin{align} T &= \frac{2m\pi ab}{h} \end{align}

From the equations for conic sections:

\begin{align} a &= \frac{\rho_c}{1-e^2}\\ b &= \frac{\rho_c}{\sqrt{1-e^2}}\\ \rho_c &= \frac{h^2}{GM} \end{align}

Thus:

\begin{align} T^2 &= \frac{4\pi^2a^3}{GM} \end{align}

The square of the orbital period is proportional to the cube of the semimajor axis.

Adding perturbations

In reality, the orbits of spacecraft are not perfectly described by Kepler's equations. This is because there exist perturbations which cause additional accelerations on the spacecraft. These perturbations come in the form of distortions to the point-mass gravitational potential that Kepler's equations assume (which then manifest as accelerations), and in the form of external forces acting on the spacecraft. The relative magnitudes of these accelerations change with altitude, as shown below. Incidentally, they also change in interesting ways with the size of the spacecraft. A centimeter or millimeter-scale spacecraft experiences perturbations that are quite different from those of large spacecraft. See Justin Atchison's thesis.

Image(filename = "perts.png", width=600, height=600)

J2 Perturbations

The above plot shows that perturbations from $J2$ are, by far, the dominant source of perturbation for spacecraft orbiting between ~400 km and Geostationary orbit. $J2$ comes from the oblateness of the Earth.

The Keplerian equations from the previous section make the assumption that the Earth's gravitational potential is given by the following equation:

\begin{align} U = -\frac{GMm}{\rho} \end{align}

This would be true if the Earth were a perfect, homogenous sphere. In reality, the Earth is neither spherical nor perfectly homogenous in density. It is lumpy. The actual gravitational sphere is approximated using spherical harmonics, shown below.

Image(filename = "model.png", width=600, height=600)

The first term in this expression should look familiar. This is the point-mass potential. The first summation is known as the zonal terms, and the last summation is known as the tesseral terms. You can see that each of the zonal terms has a term $J_n$ in the summation, and that the summation starts at 2. The $J2$ perturbations are those caused by the first element of this summation. This is the element which describes equatorial oblateness (an Earth which is fat at the equator). Higher-order terms describe more complex mass distributions and, as shown in the plot above, are less significant.

The effects of Earth's oblateness can be determined by adding the $J2$ term to the potential and solving using Lagrange's equations. The effects on the orbital parameters are given below.

\begin{align} \dot{\Omega} &= -\frac{3}{2(1-e^2)^2}nJ_2\left(\frac{R_E}{a}\right)^2 \cos{i}\\ \dot{\omega} &= \frac{3}{4(1-e^2)^2}nJ_2\left(\frac{R_e}{a}\right)^2\left(5\cos^2{i} - 1\right) \end{align}

In addition to these two orbital parameters, $J2$ also affects the mean motion:

\begin{align} \Delta n &= \frac{3}{4(1-e^2)^{\frac{3}{2}}} n J_2 \left(\frac{R_E}{a}\right)^2 \left(3\cos^2{i} - 1\right) \end{align}

These effects can be summarized as follows:

1. The orbital plane rotates (since $\dot{\Omega} \neq 0$). This is called nodal precession and is very important for sun-synchronous orbits, as we'll discuss momentarily.
2. The argument of perigee rotates within the orbital plane. This is called apsidal precession and is very important for frozen orbits (see Molniya).
3. The mean motion changes. It may be faster or slower than Keplerian depending on inclination, as shown in the equation above.

Atmospheric Drag

Below a certain altitude, atmospheric drag begins to dominate. The acceleration due to drag is modeled as:

\begin{align} a_d(r,V) &= -\frac{1}{2} \rho(r) V(r)^2 \cdot \frac{C_DA}{m} \end{align}

where $\rho(r)$ is the atmospheric density at position $r$, and $V(r)$ is the velocity of the spacecraft at position $r$. $C_D$ is the drag coefficient, $A$ the effective surface area, and $m$ the mass.

Question: For elliptical orbits, where do you expect for drag to be the most significant?

Answer: Perigee.

Orbit Design

Geostationary

The Cool Idea: Let's provide persistent, high-definition television coverage to the United States.

The Quantified Requirement: We require persistent transmission of [frequency range] radio waves to [lat/lon range] at [bandwidth]. (Not quite specific enough, but good enough for our conversation).

That's a hard problem. If you want your transmission to be received by everyone in the United States, you're either going to need a lot of transmitters, or you're going to need something high enough to see the whole geographic area that you're interested in. So, we're in the world now of spaceflight mechanics. We're going to use satellites to provide persistent coverage for this particular geographic area. Because satellites are expensive, we also want to do this with the minimum possible number of satellites.

So, this is a dead-simple example. What orbit would you design for this particular mission?

The answer: Geostationary orbit. We can park a satellite in geostationary orbit with a view of the United States and, for all time, it will just stay there happily transmitting to the United States.

If we look at a map of some of the satellites that occupy this orbit, you'll see that many of them are there to do things like we just talked about. I was specifically thinking of DirecTV in this example, which you can see here. If you go to this Wikipedia page: https://en.wikipedia.org/wiki/List_of_satellites_in_geosynchronous_orbit, you'll see that all the satellites in geosync have one of the following purposes:

1. Television and radio broadcasting (Intelsat, Yamal, DircTV, XM, etc)
2. Direct broadcasting (SES Americom, Telesat)
3. Maritime and aviation communications
4. Military communications
5. Weather

Image("Geostationary.png", width=800)

You can see that this is extremely valuable real estate. You get persistant coverage of some region of the Earth, and you can use really dumb receivers. The satellite never moves, so your receivers can just stare at one place in they sky - they don't need to track. The spacecraft act as bent pipes that receive transmissions and echo them back at a bigger region. There are a lot of politics surrounding these slots.

Molniya

The cool idea: Let's provide consistent television coverage to Russia.

The Quantified Requirement: We require persistent transmission of [some frequency] radio waves at [some bandwidth] in the latitude/longitude range that includes the Russia.

We can't use the same solution as before. Geostationary satellites are parked above the equator. For very northern and very southern regions of the Earth, these spacecraft will either be very low on the horizon, or below the horizon altogether. So, we need to apply some spaceflight mechanics.

As before, we'd like to solve this problem with the minimum necessary satellites. We want for those satellites to spend as much time as possible above the region that they're supposed to be serving - in this case Russia. I think you guys have seen this solution in this class, do you remember what the particular orbit that I'm talking about is called? Answer: Molniya.

Image("Nasa_Molniya_oblique.png")

A solution is to place the satellite on a highly elliptical orbit, and to incline the orbit such that the apogee sits above the region that it is to serve. On the first day of this class you guys likely talked about Kepler's laws. The spacecraft spends most of its time at apogee. So, if the apogee is above the region of interest, then it will spend most of its life above the region of interest. Here is the probability density function for the true anomaly of a spacecraft on a circular orbit:

\begin{align} p(\theta) = \frac{\partial{P(\theta)}}{\partial{\theta}} = \frac{(1-e)^{3/2}}{2 \pi \left(\frac{1}{e+1}\right)^{3/2} (e \cos (\theta )+1)^2} \end{align}

Substitute in values for the Molniya orbit (which we're about to solve for):

Image("plot1.png", width=800)

Here's an above-plane view of the Molniya, colorized according to probability of finding the spacecraft at that particular location:

Image("plot2.png", width=800)

So, we're definitely on the right track. So long as we choose our other orbital parameters such that apogee remains above the region of interest, then this spacecraft will spend the majority of its time over the region of interest. We've introduced a few more layers of complication, however, because we now have an elliptical, inclined orbit. So, that orbit is going to have both nodal and apsidal precession due to Earth's oblateness. We need to deal with that.

Apsidal precession

The perigee of an elliptical orbit around an oblate body will precess. So, if we're not careful, then we'll eventually end up with our satellite spending most of its time over the southern hemisphere rather than over the northern hemisphere. The rate of apsidal precession (only including the first, most significant J-term) is given by:

\begin{align} \dot{\omega} = \frac{3}{2}\cdot n J_2 \cdot \left(\frac{R_E}{a}\right)^2 \frac{2-2.5\sin^2{i}}{\left(1-e^2\right)^2} \end{align}

If you take a look at this equation, how would you solve the problem of apsidal precession? You could make the term $2-2.5\sin^2{i}=0$. If you solve that for $i$, you'll find an inclination of 63.4 degrees.

\begin{align} \sin^2{i} &= \frac{2}{2.5}\\ \sin{i} &= \sqrt{\frac{2}{2.5}}\\ i &= \sin^{-1}\left(\sqrt{\frac{2}{2.5}}\right)\\ &= 63.4\text{ degrees} \end{align}

So, if we put the spacecraft on an orbit with an inclination of 63.4 degrees, then our apogee won't wander out of the northern hemisphere. This is a frozen orbit.

Put another way, this choice of inclination fixes our apogee in latitude, but it does not fix our apogee in longitude.

Think for a second about how cool that is.

Nodal precession

The Earth's oblateness has another effect of exerting a torque on the orbit. Because the spacecraft has angular momentum, however, this torque does not result in an inclination change, but instead a precession of the right ascension of the ascending node. In other words, the ground-track drifts as our apogee wanders to other longitudes.

\begin{align} \dot{\Omega} &= -\frac{3}{2} \cdot nJ_2 \cdot \left(\frac{R_E}{a}\right)^2 \frac{\cos{i}}{\left(1-e^2\right)^2} \end{align}

There's not much for us to play with in this equation. Our inclination is fixed in order to lock our apogee latitude, so we can't change that. Our semimajor axis and our eccentricity both come from our apogee/perigee altitudes. We want the eccentricity to be as big as we can, so we make our perigee as low as we can while avoiding too much atmospheric drag. So, the only degree of freedom that we have to play with is our apogee altitude.

The nodal period of the satellite (the time between ascending nodes) is approximately given by:

\begin{align} T &= \frac{2\pi}{n + \dot{\omega}} \end{align}

Where $n$ is the mean motion of the satellite (rad/sec) and $\dot{\omega}$ is the rate of change of the argument of perigee, as given above and rewritten below:

\begin{align} \dot{\omega} = \frac{3}{2}\cdot n J_2 \cdot \left(\frac{R_E}{a}\right)^2 \frac{2-2.5\sin^2{i}}{\left(1-e^2\right)^2} \end{align}

So, $T$ tells us the amount of time between ascending nodes. We want to relate that to the Earth's rotation time, since we're trying to fix the ground track of the spacecraft. Let's call the angular rate of the Earth (relative to far away stars) $\dot{\Omega}_E$. We can then use the rate of change of the right ascension of the ascending node to solve for the rotation rate of the Earth with respect to the satellite's orbital plane:

\begin{align} \omega_{E/op} &= \dot{\Omega}_E - \dot{\Omega} \end{align}

We want for the satellite to complete $m$ (in this case, 2) orbits in the same amount of time that it takes for the Earth to turn once. That means:

\begin{align} mT &= \frac{2\pi}{\dot{\Omega}_E - \dot{\Omega}} \end{align}

Substituting for $T$:

\begin{align} m\frac{2\pi}{n + \dot{\omega}} &= \frac{2\pi}{\dot{\Omega}_E - \dot{\Omega}} \end{align}

Simplify:

\begin{align} n + \dot{\omega} &= m \left(\dot{\Omega}_E - \dot{\Omega}\right) \end{align}

Our judicious choice of inclination (previous section) makes $\dot{\omega} \approx 0$. So:

\begin{align} n &= m\left(\dot{\Omega}_E - \dot{\Omega}\right) \end{align}

We furthermore assume a perigee of $a(1-e)=R_E+600$ km and, for our case, $m=2$ satellite orbits per Earth rotation. Then, the above equation can be solved iteratively for the apogee $a(1+e)$. At the solved-for apogee altitude, the orbital period of the spacecraft will cancel with nodal precession, and the ground-track will not drift in longitude. Obviously there are going to be other perturbations, so maintenance will be required, but you will have cleverly avoided having to deal with all of those perturbations. https://journals.ametsoc.org/doi/pdf/10.1175/1520-0426%281990%29007%3C0517%3AOTUOSI%3E2.0.CO%3B2

This technique is generally useful for repeat ground-track orbits.

The Result

We have frozen the latitude of the apogee by careful selection of inclination, and we froze the longitude of the apogee by careful selection of orbital period (which really means careful selection of apogee altitude, given perigee altitude). Finally, we want to make certain that the apogee of the spacecraft is at the most northern point in its orbit, so this fixes our argument of perigee to 270 degrees. Here are the parameters that we've come up with:

1. Inclination of 63.4 degrees (to freeze latitude of apogee)
2. Perigee at 600 km (as low as possible, so that our apogee can be as high as possible)
3. Apogee at ~39,700 km (for a semi-major axis which gives an orbital period of exactly 1/2 days for non-drifting longitude of ground-track)
4. Eccentricity of 0.74, as calculated from apogee/perigee
5. Argument of perigee at 270 so that the perigee is at northern-most point.

Here's our ground track:

Image("Molniya.jpg")

POV from spacecraft:

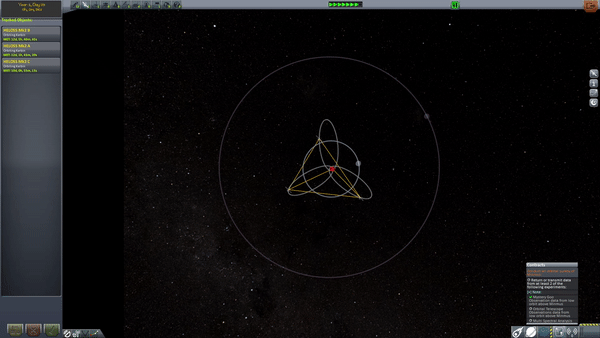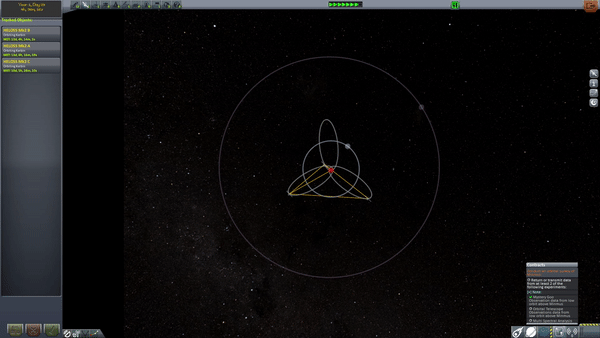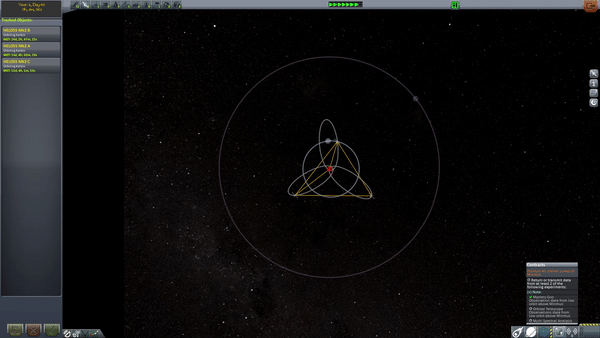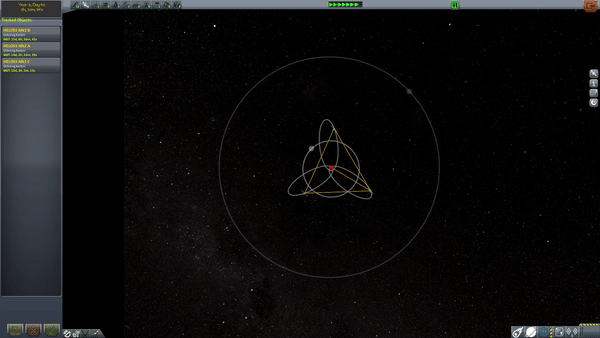
There's still a problem to solve. The satellite spends about 2/3 of its time north of the horizontal line which slices the ground-track loops in half. So, it only spends 1/3 of its time (8 hours/day) over the region of interest, in this case Russia.

We need more satellites. We can use 3 satellites on identical orbits, but with longitude of ascending nodes separated by 120 degrees and phased such that their apogees are just under 8 hours apart from one another. then, we get continous coverage. Your receivers need to track the satellites and switch among them, but you've got coverage. (Think about what happens to the ground track of each satellites as you slide its longitude of ascending node, and as you change its true anomaly).

By the way

There's a very similar orbit, called a Tundra orbit, which uses exactly the same philosophy as the Molniya but uses a period of exactly 1 Earth rotation ($m=1$, in the above equation). What would the ground track for a spacecraft on that orbit look like?

Image("Tundra.jpg")

Something to think about: What if you had to send signals to your satellites from handheld receivers? Would this orbit still work?

Sun Synchronous Orbit

A Sun Synchronous Orbit is one where the precession of the right ascension of the ascending node exactly matches the rotation of the Earth around the Sun, as shown below. We can accomplish this by choosing $a$ and $i$ such that $\dot{\Omega}$ exactly equals the rotation rate of the Earth.

\begin{align} \dot{\Omega} &= -\frac{3}{2(1-e^2)^2}nJ_2\left(\frac{R_E}{a}\right)^2 \cos{i} = \frac{2\pi}{365 \cdot 86400} \end{align}

Image("Sun.png")

Constellation Design

GPS

Cool idea: Let's create a global positioning system.

Quantified: (I'm skipping over the technical steps associated with GPS, to get directly to the constellation requirement). We require at least 4 satellites to be in view (15 deg above the horizon) at any time from any location on the Earth.

I'm going to cheat a bit with this. For the previous situations, we started with the requirements and (waving our hands a lot) derived the orbital parameters and configurations. In this case, I'm going to start by showing you the orbital configuration and show that it meets the requirements. There's not one right answer for meeting that requirement, so I think this is what makes sense for this example.

The constellation is shown above. I'll describe it, then we'll consider its features one at a time.

It is composed of (at minimum) 24 satellites (there are spares) on 6 orbital planes. Each of these planes is at an inclination of approximately 55 degrees, and each is separated by 60 deg in the right ascension of the ascending node (evenly spaced around the Earth, 60*6=360 degrees). The orbital period is, like the Molniya orbit, one half of a sidereal day. The orbits are very close to circular. There are four spacecraft on each orbital plane. They are not evenly separated. The angular difference between satellites in each orbit is approximately 30 deg, 105 deg, 120 deg, and 105 deg.

Let's walk through each feature of this constellation and show what it gets us.

High-Level Goals

1. Design a constellation that meets requirements
2. Design the constellation such that perturbations do not warp the constellation in ways that make it no longer meet requirements

Observation

Do you see how symmetry is an important element of this requirement?

Circular Orbits

How does this help meet requirements?

As we talked about, there isn't only one configuration that meets these requirements, and some of those configurations will use spacecraft on elliptical orbits. However, there are some nice properties introduced by circular orbits.

There's a notion of symmetry built into the requirement of 4 spacecraft being in view "from anywhere on Earth." In other words, there should be no preferred location on Earth where coverage is better than elsewhere. The constellation should treat all locations on the surface of the Earth the same.

Elliptical orbits have preferred locations. That's why we utilized them for the Molniya configurations. There are places in elliptical orbits where the spacecraft spends more time.

This isn't true for circular orbits. Every true anomaly within that orbit is symmetric - there's no preferred location for the spacecraft. Since that orbit goes around the center of the Earth, this means that every location that passes within range of a particular spacecraft is treated equivalently.

Something to think about: If the coverage requirement were USA-specific, would you still use circular orbits?

How does this help preserve the structure of the constellation?

With circular orbits, we don't need to worry about apsidal precession introducing a time-varying element to the orbital configurations.

Semi-synchronous orbital period

How does this help meet requirements?

Like in the Molniya constellation, each spacecraft in the GPS constellation is at an altitude that gives it an orbital period which is exactly 1/2 the time that it takes for the Earth to complete one rotation. That is, the spacecraft orbits twice everytime the Earth rotates once.

This places the GPS satellites at a high enough altitude for them to have good visibility of much of the Earth (78 percent the hemisphere is visible to each satellite). The higher the spacecraft is, the more of the Earth can see that spacecraft, and the less spacecraft you need. However, the higher you get the farther you need to transmit. That either means you need more powerful (more expensive) spacecraft, or more sophisticated receivers. It's a trade-off. Medium-Earth orbit is a nice compromise between number of required spacecraft and expense of each spacecraft.

How does this help preserve the structure of the constellation?

This keeps the ground track relatively constant for each spacecraft. For GPS to work properly, each receiver needs to know exactly (exactly) where the spacecraft is located. Even in the semisynchronous orbit, a lot of modeling of all the perturbations is required in order to maintain a precise-enough estimate for spacecraft position.

But, there is some determinism associated with having persistent ground tracks. This was very helpful during development because even with only four satellites, correct alignment means all four are visible from one spot for a few hours each day. For military operations, the ground track repeat can be used to ensure good coverage in combat zones. (Got that from Wikipedia)

6 orbital planes

How does this help meet requirements?

I don't know why exactly the number 6 was chosen. Clearly, there is some minimum number of orbital planes that is required for persistent global coverage. If you put all the spacecraft on one plane, then there would be parts of the world that wouldn't be able to see any of the satellites at any particular moment in time. That's clear, right?

I think the minimum number of planes at GPS altitude is 3, though I'm not certain. You may wonder why not just put each satellite on its own plane. I suspect that this has more to do with constellation maintenance. It's quite easy to move spacecraft within an orbital plane, and much more difficult to move them out of plane. So, with multiple spacecraft on the same plane, you can deploy orbiting spares that can easily move into the correct location if a spacecraft breaks. I'm speculating though, I'm not actually sure. Do any of you know?

More planes may also help reduce geometric dilution of precision.

How does this help preserve the structure of the constellation?

Just having 6 planes doesn't, really. But, the arrangement of those planes (next 2 sections) does.

60 deg separation in right ascesion of ascending node

How does this help meet requirements?

Here too is a symmetry. We want coverage everywhere on the globe. By separating each orbital plane by 60 degrees, we evenly distribute the ground tracks for the GPS satellites across longitudes. If instead we clustered them, then we'd get preferential coverage in regions near the ground tracks.

How does this help preserve the structure of the constellation?

Doesn't help or hurt.

55 deg of inclination

How does this help meet requirements?

We're aiming for global coverage. At 55 degrees and an orbital radius of 26,560 km, the constellation has a continuous view of the entire globe. At lower inclinations, the constellation would not be able to see the whole globe. At lower altitudes at this inclination, the constellation would not be able to see the entire globe.

How does this help preserve the structure of the constellation?

In general, this neither helps nor hurts. Because all of the orbits are at the same inclination, the perturbing forces that they experience from J2 are all the same. So, if the whole constellation were to precess nodeally, it would precess together and maintain its structure. But, so far as I could figure out, each has an orbital period to cancel much of this precession in the same way that Molniya does. So, each ground track is essentially fixed and maintained if it wanders.

>=24 satellites, unequally spaced

In order to guarantee at least 4 spacecraft are always in view in this configuration, you need at least 24 satellites. If these satellites were equally spaced, then the expected number of satellites in view at a given latitude would be constant, regardless of longitude. However, the 4 satellites along each orbit are not equally spaced.

This is the first symmetry break that we've seen for this constellation.

On each orbit, the angular spacing between satellites is approximately 30, 105, 120, 105 degrees. Recall that each satellite can see approximately 78 percent of the hemisphere of the Earth. So, from the surface of the Earth, the number of visible satellites is expected to be (approximately):

\begin{align} 24 \cdot \frac{1}{2} \cdot 0.78 = 9.36 \end{align}

However, because the spacecraft are differentially spaced, this number may drop as low as 5 and go as high as 12. I found one resource that suggested that this arrangement keeps the expected number over the United States higher (8-12) than elsewhere. Potentially this arrangement just leads to better global coverage also. I'm not sure, I couldn't find much information on this. If any of you know, let me know.

Iridium

The cool idea: Let's provide voice and data coverage to cell phones and pagers over the entire Earth's surface.

I'm not going to jump straight to a more quantified requirement statement this time. Let's see if we can reason our way to some of these requirements ourselves. In the previous example (GPS), the satellites did not need to receive data from the receivers. They're just beacons. In this case, we want to send data to the Iridium satellites via handheld devices so that they can send it elsewhere. What does that place a constraint on? Answer: altitude.

If we want for our satellite phones to be handheld and to have a reasonable data rate, we benefit from having the spacecraft closer to the phone. The GPS satellites are over 20,000 km away. Iridium, by contrast, is about 480 km. That's still far, but not nearly as far. We can give ourselves a distance-to-phone requirement.

Problem statement: Provide persistent coverage for data transmission at [bandwidth] from anywhere on the Earth to anywhere on the Earth at [latency]. Our distance requirement is hidden in the bandwidth requirement.

The field of regard of our constellation is the same as it was for GPS (the whole planet), but now our spacecraft are in low-Earth orbit. So, the field of view of each spacecraft is much smaller. What is that going to mean? More spacecraft. Furthermore, because we want global coverage from spacecraft in low orbits with small fields of view, what sort of inclination will you expect that at least some of the spacecraft will have? Answer: very high, so that they can cover the poles.

I'm going to do the same thing that I did with GPS, and show you the constellation first, then talk through its features. Here's what the constellation looks like:

Notice how the spacecraft are phased such that the circles of coverage overlap for total coverage. With different phasing, this would not be the case.

The Iridium constellation is composed of 66 satellites (plus spares) arranged into 6 orbital planes with 11 satellites on each plane. Each plane has an inclination of 86.4 degrees. The orbits are all circular. As before, let's walk through these features. Iridium gets to use the GPS constellation.

High-Level Goals

1. Design a constellation that meets requirements
2. Design the constellation such that perturbations do not warp the constellation in ways that make it no longer meet requirements

Circular Orbits

How does this help meet requirements?

As with GPS, Iridium does not want to have preferential coverage anyplace on the Earth. By placing all of the spacecraft on circular orbits, and evenly distributing them along those orbits, then every part of the Earth (at a particular latitude) will have the same coverage.

How does this help preserve the structure of the constellation?

As before, we've eliminated apsidal precession as a concern.

6 orbital planes, 60 deg of separation in longitude of ascending node

How does this help meet requirements?

As evidenced by the animation, this is the amount that is required at the Iridium altitude. The altitude is fixed by the ability of the cell phones to transmit. In order to adequately cover the Earth with the reduced field of view of each spacecraft, you need to have 6 orbital planes, 11 spacecraft on each orbit. You need to evenly distribute those planes.

When Iridium first came around, they thought they would need 7 planes, which would lead to 77 spacecraft. That's where the name "Iridium" comes from. It's the element with atomic number 77.

How does this help preserve the structure of the constellation?

Just having 6 planes doesn't, really. But, the arrangement of those planes does.

86.4 deg of inclination

How does this help meet requirements?

These are essentially polar orbits. At such low altitude, orbits of this extreme inclination are required in order to provide global coverage. At lower inclinations, the constellation would be unable to provide coverage near the poles. Not that that would be a tremendously big deal, because there aren't that many people living in those areas, but there you go.

How does this help preserve the structure of the constellation?

As with GPS, the Iridium spacecraft perform orbital maintenance with onboard thrusters. However, because all orbits share the same inclination, many of these perturbing forces are the same for all orbits. So, if left alone, the collection would nodally precess together. Of course other perturbations would eventually turn it into a mess.

Routing

How it works

Each spacecraft in the Iridium network maintains a connection to four other spacecraft: the two in front/behind on the same orbit, and one on each adjacent orbital plane. See below.

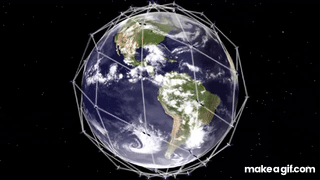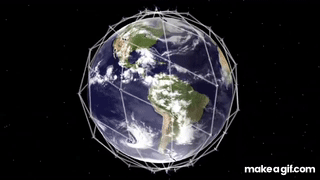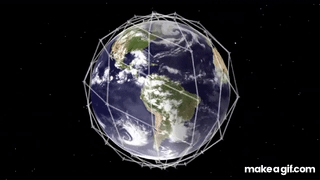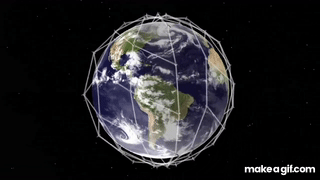
At their altitude, each Iridium spacecraft only remains within view for, at most, 7 minutes. As the spacecraft passes out of range, the communication link is transferred to the adjacent spacecraft which is coming into view. If such a handoff cannot be made (perhaps an obstacle is in the way), then the call is dropped.

The precise routing mechanism used by the Iridium network is proprietary. However, they have a few things to take advantage of:

1. We have access to GPS information
2. Our nearest neighbors are constant (they change position, but they're the same neighbors)
3. Though the network is dynamic, the structure is invariant. This is a predictable dynamic network

Problems

As you can see in the animation, half of the spacecraft are moving up at any moment in time, and the other half are moving down. This creates a seam. The Iridium satellites cannot route across this seam so, sometimes, folks that are very close geographically will have a long amount of latency because the packet is routed all the way around the globe.

Starlink

The cool idea: Let's provide internet to most of the world.

We cannot get into nearly as much detail with Starlink, because not as much information is available. But it's too cool not to talk about.

There is a publically available FCC application with some details. Here's that FCC documentation, in case you'd like to read through it: https://fcc.report/IBFS/SAT-MOD-20181108-00083/1569860.pdf. I think this document is out-of-date, so some of the information that I'll relate will also be out-of-date. But that's ok.

Here's the plan, as of 2016. This has changed a bit since then:

Image("Plan.png")

Here is an animation of the Phase 1 deployment. You can see that things are different between this animation and the FCC documentation. This animation shows 1584 spacecraft on 24 orbital planes, the documentation calls for 1600 satellites on 32 orbital planes. The animation is more up-to-date.

The plan, as far as I know, is to use lasers to communicate among the spacecraft. Like in the Iridium constellation, each spacecraft will have a connection to the spacecraft immediately in front and behind it on the same orbital plane. Furthermore, each will have a connection to a spacecraft on each adjacent orbital plane. I do not know if they will be attempting connections between spacecraft that pass one another moving north/south. Do any of you know?

You can see in the animation that this sort of connectivity facilitates very efficient movement of data in the East-West direction. That is, as far as I can tell, the primary goal of this first deployment. You can also see that SpaceX is not providing coverage to northern/southern latitudes in this first deployment, that will come later. My expectation is that the routing policy will tend to route among spacecraft which are in phase with one another. North-south routes will require an east or west route to get on the proper northeast/southeast orbital plane, and then routing along that plane.

The fundamental insight (again, I think) from the business-model perspective is that light travels faster in vaccuum than it does in fiber-optic cables. So, with enough spacecraft in the proper orbits and with an adequate routing strategy, you can decrease latency of information transmission over large distances to below that which is possible with the internet, or even theoretically possible with fiber optic cables. If you're doing high-speed trading, you're willing to pay a lot for that decrease in latency.

And it's no accident that phase 1 will decrease latency in the East-west directions. That means New York, San Francisco, London, and China. They are prioritizing latency decreases among the population centers that will pay the most for that capability.