See also: the fixed point webpage on the course website. Contains more information about the stdfix.h types, performance metrics, and other custom fix types than that considered below.
Video discussion of content on this page¶
What's the point of fixed point?¶
Fixed point is the solution to a problem.
Problem: I want to do arithmetic with fractional resolution but I can't afford the CPU cycles to use floating point.
Solution: Fixed point.
Recalling signed int¶
I think the most intuitive way to introduce fixed point is to first remind you about integers.
Let us recall a signed int. An int has 32 bits. Because this is a signed (2’s complement) int, the top bit is reserved for sign information. That means we have 31 bits of value, and we can store values in the range of +/- $2^{31}$. The bottommost bit represents $2^0$, the next $2^1$, etc, etc, up to the second-to-topmost bit which represents $2^{30}$. We could think about the decimal point for the numbers represented by this int to be below the bottom bit. Because the resolution of an int is $2^0$, or 1, we can only represent integer values.

Introducing fixed point¶
To make a fixed point number, all that we do is place this decimal somewhere in the middle. As an example, we’ll decide that the decimal point is between bits 14 and 15. Mostly, this is just the way that we now think about this number and the CPU doesn’t know the difference. However, there are a few special cases that we need to think about so that the CPU treats this number properly.
What are the consequences of this? Our range has been reduced to +/-$2^{16}$, but, we can now store values with a resolution down to $2^{-15}$. We've traded range for resolution.

The CPU still sees a signed int. In fact, to create a data type which will call fix, we would just do the following:
typedef signed int fix
Arithemetic with fixed point¶
Some of the standard arithmetic operations work on our new fix datatype without any modifications. Others requires a little bit of care. Let's consider each.
Addition/subtraction¶
Addition and subtraction just work. The CPU has a 2's complement hardware adder, these additions and subtractions behave the same as always, despite the fact that we've placed the decimal elsewhere in the bitstring. So, something like the following is perfectly acceptable (we're going to consider those int2fix type conversions in a later section):
fix var1 = int2fix(50) ;
fix var2 = int2fix(30) ;
fix var3 = var1 + var2 ;
Multiplication¶
Suppose that we multiply two 32-bit values. We will get an intermediate value that is 64-bits long. If each of these values were signed 16.15 fixed point (1 sign, 16 integer, 15 fraction), where is the decimal point in this intermediate variable? It’s right above bit 29. If you multiply two fixed point values, each of which with 17 bits above the decimal (16 integer and 1 sign) and 15 bits below the decimal, then we end up with an intermediate value that has 2x17 = 34 bits above the decimal, and 2x15 = 30 bits below the decimal, for a total length of 64 bits.
Now, which of these do we actually care about? We want the output of this multiplication to also be a signed 16.15 fixed point, so we care about the bits that immediately surround the decimal point. Everything below that is underflow, which is ignored. And we better not have anything up here above the region of interest, because that means we’ve overflowed the representation. So, we care about these bits which hug the decimal. Multiply will not work if the number is too big. Remember that range check in the Boids pseudocode? This is why we do that.
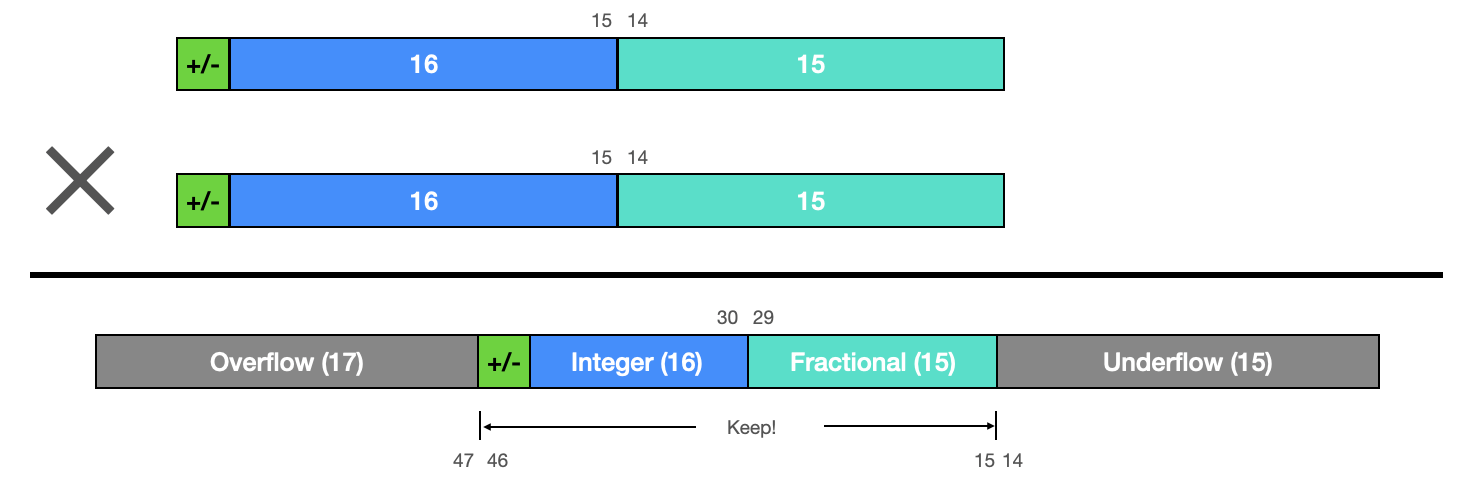
In order to perform this multiplication and retain the range of bits that are relevant, we will do the following:
- Typecast each
fixtolong long(64 bits) - Multiply them, yielding the 64-bit intermediate variable illustrated above
- Right-shift by 15 to shift out the underflow
- Typecast back to
fixto retain only the least significant 32 bits, getting rid of the overflow. The result will be a 32-bit fixed point variable with the decimal precisely where we want it - between bits 14 and 15.
In code, that looks like the following. This is implemented as a macro because that's faster than a function.
#define multfix(a,b) ((fix))(((( signed long long a))*((signed long long b)) >> 15))
By the way, what would change if we had placed the decimal elsewhere in the bitstring, perhaps between bits 19 and 20? The shift-right would be a different value. We've used integer multiplication, which is fast, but we're maintaining fractional resolution. That's cool.
Division¶
The macro for division is given below, but avoid these if at all possible. Division is very slow.
#define divfix(a,b) ((fix)(((( signed long long)(a) << 15 / (b)))
Type conversion to and from fix¶
int to and from fix¶
Conversions from fix to int and from int to fix are just shifts! If you look at what each bit for each data type represents, this becomes clear:
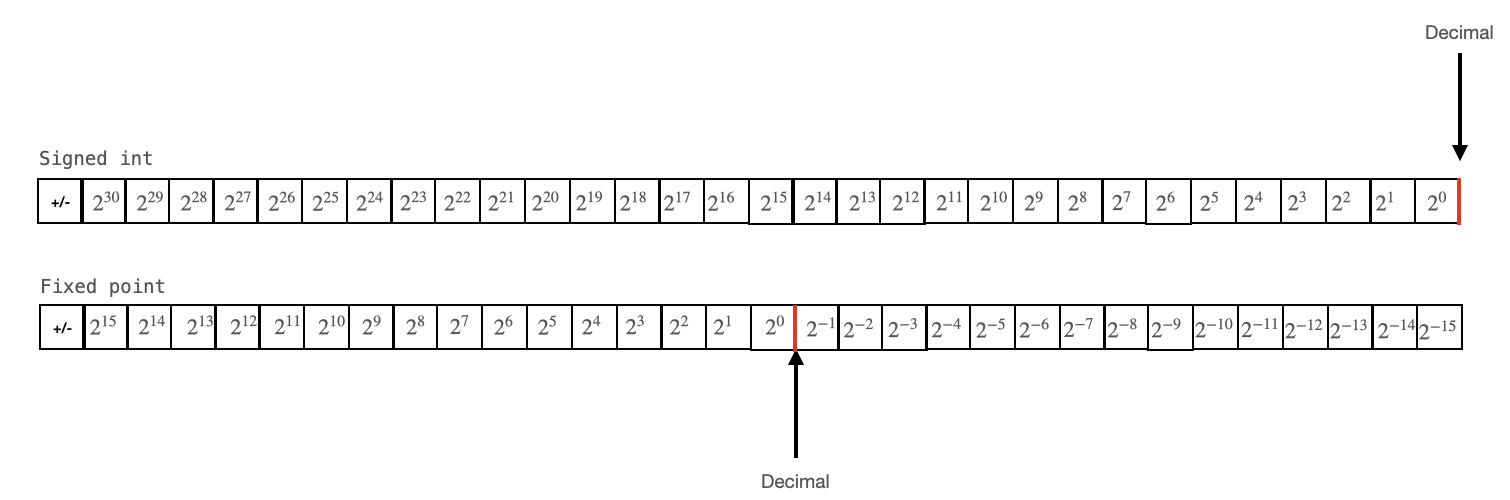
In order to convert between these two types, we simply shift the decimal point from wherever it is to wherever it needs to be. For the fix we've been considering (with the decimal between bits 14 and 15), this looks like the following:
#define int2fix(a) ((fix))((a) << 15))
#define fix2int(a) ((int))((a >> 15))
float to and from fix¶
I think the most intuitive way to think about conversions between float and fix is to think about unit conversions and dimensional analysis. Consider how we represent the value 1 with a fix. For our choice of decimal location, this would be represented by a 1 in the 15th bit, and 0's in all other bits.
The CPU sees that as the value $2^{15}$, or $32768$. So 1 unit of fixed point is $2^{15}$ units of int. Very similarly to 1 unit of kilometers is 1000 units of meters. We can convert between these two data types by doing dimensional analysis, as shown below:
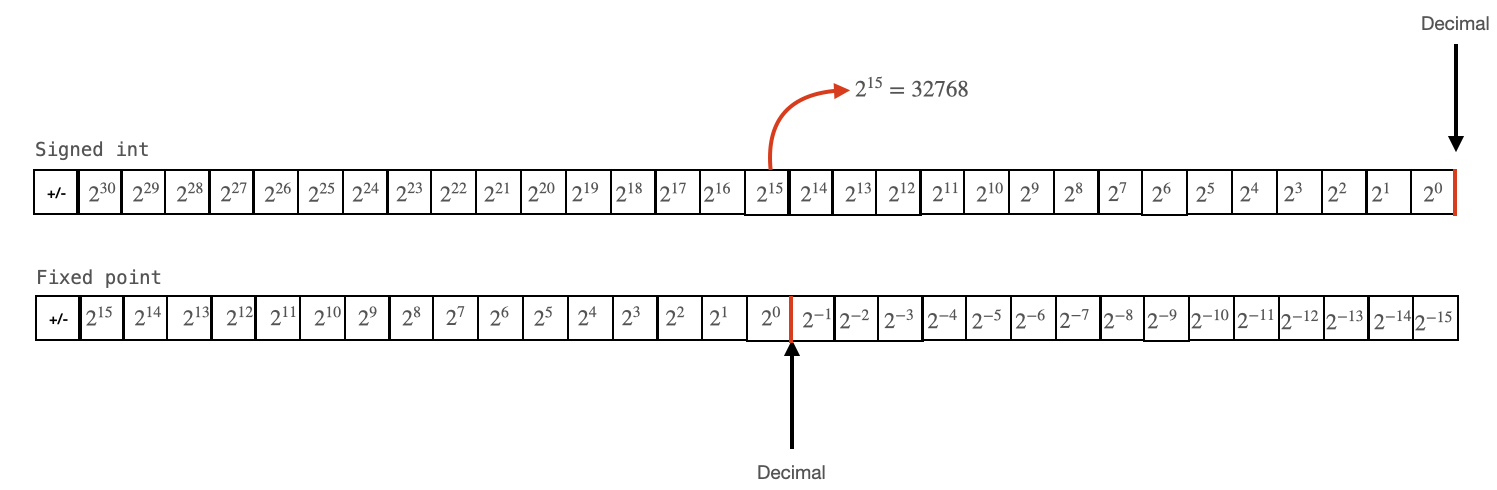
This gets encoded as the following:
#define float2fix(a) ((fix))(a * 32768.0)
#define fix2float(a) ((float)(a) / 32768.0)
How would this change if we placed the decimal elsewhere? The 32768.0 would be some other value. Note that there are floating point operations in both of these conversions! So, you only want to use these conversions during setup, you don’t want to be calling macros like this during an animation loop because it will slow everything down considerably. Do all of your animation arithmetic in fixed point.
Some other operations¶
Absolute value¶
Just works! You can call abs() as usual.
Square root¶
Square root is an interesting case. It is actually fastest to convert your fixed point value to a float, calculate the square root of that floating point value, and then convert the result of that calculation back into a fix, as shown below.
#define sqrtfix(a) (float2fix(sqrt(fix2float(a)))
This, by the way, is still slow compared to fixed multiplies. But why this is the case is interesting. If you look at IEEE floating point format, the significant, exponent, and sign are all stored separately. 24 bits of significant, 8 bits of exponent, 1 bit of sign. So, a float square root is fast (relatively speaking) because it involves a right-shift of the exponent part of the representation.
There is, by the way, a crazy fast floating point square root that computer graphics people use. The fast inverse square root was used famously in the video game Quake to do lots and lots of divisions by root distance to get lighting to look right. It calculates 1/sqrt(x) using only multiplications and bit shift operations. Bit shift operations . . . on a floating point number.
For those of you that like this stuff, there are whole webpages of bit twiddling tricks that are just amazing. https://graphics.stanford.edu/~seander/bithacks.html. Swapping values, modulus devision, computing log base 2 or 10. Really fun tricks.
Random number generation in fixed point¶
Random number generation in fixed point is mercifully easy, we just need to be cognizant of where we shift randomly generated bits in order to generate a number in our desired range.
The standard function rand() will return a uniformly distributed pseudorandom number between 0 and 65536. That is to say, it generates a random 16-bit short. If we cast this randomly generated value to a fix, we will move the randomly generated bits up to bits 31:16. If we wanted for the randomly generated fix to be in the range [0, 1], then we want for bits 15:0 to contain the randomly generated bits. So, we right-shift this value so that the information in bit 31 lands in bit 15, and the information in bit 16 lands in bit 0. That means we right-shift by 16, as shown below:
Random fix between 0 and 1
rand_fix = (fix)(rand() & 0xffff) >> 16 ;
What if we want a random number between -1 and 1. We would then shift by 15 instead of 16 (which would give a random number between 0 and 2) and then subtract 1. See below:
Random fix between -1 and 1
rand_fix = ((fix)(rand() & 0xffff) >> 15) - 1 ;
Similarly for -2, 2:
Random fix between -2 and 2
rand_fix = ((fix)(rand() & 0xffff) >> 14) - 2 ;
And you can do additional combinations. If you wanted a value between -1.5 and 1.5, you would generate a number in the range [0, 2], add a second number in the range [0, 1], and then subtract 1.5:
Random fix between -1.5 and 1.5
rand_fix = ((fix)(rand() & 0xffff) >> 15) + ((fix)(rand() & 0xffff) >> 16) - 1.5 ;
stdfix.h¶
If you #include <stdfix.h>, you gain access to compiler-understood fixed-point data types. For example, you get access to type _Accum, which is a 16.15 fixed point exactly like the one that we've been considering above. That means that you can use all the ordinary symbols for arithmetic, and fixed point arithmetic will just be applied behind the scenes. If your application supports the range and resolution offered by one of these types, use them! Then you don't need to write all the routines considered above.
Demonstration¶
In the video below, each core of the RP2040 computes half of the Mandelbrot set. One core computes the top half of the set using fixed point, and the other core computes the bottom half using floating point. On this particular system, there is an approximately 5.3x speedup using fixed point.