Bayesian search: chipsats to Dyson spheres¶
V. Hunter Adams¶
- Why I put this together
- Introduction and background
- A toy example
- Generalizing to Dyson spheres
- Where we begin for Dyson spheres
- Incorporating expert knowledge to inform location probabilities for Dyson spheres
- Incorporating expert knowledge on searchability for Dyson spheres
- Prioritizing search for Dyson spheres
- Updating our knowledge after a search for Dyson spheres
- A north wind blows for Dyson spheres
- Updating our prioritized search for Dyson spheres
- Some thoughts on prior probabilities
- Some thoughts on searchability
- Historical precedent for Bayesian search
Why I put this together¶
I'm still reeling from the Dyson Minds workshop. In particular, I've been pondering the extent to which the rapid and properly-weighted incorporation of so many sources of information may be one of the first puzzles to solve. These sources of information include expert opinion from physicists, astronomers, engineers, philosophers, etc. They also include publications of relevance, and expert opinion on the relative searchability of various corners of the cosmos. That's a lot of stuff! We may benefit from a formalized search infrastructure. I put together this document to propose one such infrastructure.
The Bayesian search formulation grids up the universe and, for each location in that grid, computes the equation below. The advantages of formulating our search in this way include:
- Rapid integration of all information sources to the problem of search. By localizing each new piece of information to one of the terms in the below equation, they can always be directly applied to informing the actual search for these structures. All information contributes ultimately to answering the question "where are we most likely to find a Dyson sphere?"
- Facilitation of interdisciplinary conversation. It gives highly diverse experts a shared interface for discussing and debating the topic. Astrophysicists, philosophers, etc. can apply their domain knowledge to the question of probability. And probabilities can be combined really nicely. For instance, folks of various domains could discuss among themselves the probability of existence from their own field's perspective, and then we could have an interdisciplinary conversation that discusses the independence or non-independence of those probabilities.
- This allows for our conversations to meaningfully include the perspectives of people that strongly believe Dyson sphere's don't exist. Their perspective can be incorporated as easily as any other in the probability of existence conversation.
- This formalism may be well-suited to AI assistance. I could imagine using an AI to help translate information to probabilities for incorporation into the model.
- Recomputing the probability map is a trivially parallizable process, which may be accelerated by a massively parallel computer that may or may not be sitting around looking for an application ;)
- Many intuitions (e.g. that we should look through data that we've already gathered, and that we should focus our search in places that we can easily get good data) emerge from this framework.
- This framework not only tells us where Dyson spheres are most likely located, but also tells us where we are most likely to find them. These may be very different locations!
- Future workshops can by highly targeted, with easy-to-quantify-and-visualize progress metrics.
The outcome of this formulation is a heatmap of the sky that shows the most likely locations for Dyson spheres, incorporating all information of relevance to that search. With any new information of relevance (someone publishes a paper, an expert expresses an opinion, we get some new data, we parse some old data, etc.), the map updates.
Introduction and background¶
In graduate school, I did a lot of work on estimation, which attempts to use every shred of available information in order to generate the best-possible guess for some quantity. Estimators like Kalman filters are famously used for estimating spacecraft state, and it is in this context that I was introduced to the field. But the utility of estimation extends well beyond spacecraft engineering. More recently, I've applied these techniques to studying differences in proportions in survey data, generating a communication strategy for Breakthrough Starshot (I think this is a practical solution, though that is not a universally shared opinion), and doing probabilistic radio decoding.
Indeed, all of these estimators are simply applications of Bayes' Theorem, which applies anytime one is attempting to determine the probability of each possible cause for a measured effect. In the case of spacecraft state estimation, we ask "which is the most probable of all possible spacecraft rotation rates, given the gyro measurement and what we know about rigid body dyamics?" But the same mathematical infrastructure can be applied to lots of other things, including search. I've been doing this lately for a different project, but I think the approach could be of a lot of relevance to the hunt for Dyson spheres.
Applied to search, the question we ask is "what is the most likely location of what we're trying to find, given . . .":
- The probability of what we're looking for being in each possible location.
- The probability of seeing what we're looking for, even if we search in the correct location.
By gridding-up our search space and assigning a value for each of the above probabilities for each cell in that grid-space, we can generate a heatmap that describes where what we're looking for is most likely to be, given everything that we know about the problem. That is, this infrastructure incorporates all prior information about the location of the object, and it incorporates information about differences in observability for the object at different locations. I think this could be a useful way for us to incorporate highly varied domain knowledge to the search for Dyson sphere, and for us to quantify and visualize our increases in information.
A toy example¶
I'm going to walk through this example, and then in a subsequent section I'll discuss how each step of this process generalizes to the search for Dyson spheres. Perhaps starting with a terrestrial example helps build intuition.
Problem statement: A chipsat has descended from space and landed somewhere in or near Cayuga Lake, and we'd like to find it.
Where we begin¶
With only the above problem statement, we've no reason to prefer one location to another in order to begin our search. That is to say, within our searchspace, the probability mass distribution for the chipsat is uniform. In the figure below, we see a totally uniform probability mass distribution for our searchspace. No location is more likely than any other.

Incorporating expert knowledge to inform location probabilities¶
But, before we even start looking for the chipsat, we can apply things that we know about how things fall from space. Let us suppose that we knew the chipsat's position and velocity when it hit the top of the atmosphere. We can't use that information to locate the chipsat, because it will have been blown about by the hard-to-predict atmosphere, and flopped around chaotically, but we can at very least adjust our probabilities such that they incorporate this knowledge.

$p(\text{chipsat location})$
Incorporating expert knowledge on searchability¶
Not all of the locations in our searchspace are equally searchable! For each gridcell in our searchspace, there is some probability that we don't find the chipsat even if we search there. Some of these cells will include dense foliage or treacherous gorges. We could look there, and the chipsat could be there, and we'd still be really unlikely to find it.
Let us suppose that this landing ellipse aligns with Cayuga Lake. For purposes of this discussion, we'll suppose that the shores of the lake are very searchable (it's easy to find a chipsat on the beach). We'll suppose that the water itself is moderately searchable, and that the land has low searchability. We might imagine that this is because much of it is private and hard to access, or difficult to navigate, or whatever.

$p(\text{not finding chipsat in gridcell}|\text{it is located in that gridcell})$
Prioritizing search¶
Provided the prior distribution on chipsat location, and the probability of not finding the chipsat at a particular location were we to look there, we can compute the probability that we find the chipsat at each location in the searchspace. This can help prioritize our search, since we should be looking in the places where we are most likely to find what we're looking for, which aren't necessarily the places where it's most likely located.
It should match intuition that a policy which prioritizes searching the lake and its shores emerges. These are the places where we are most likely to find what we're looking for.

$p(\text{chipsat is in gridcell})\cdot p(\text{finding chipsat in that gridcell})$
Updating our knowledge after a search¶
Let us suppose that, by way of a tremendous effort, we rapidly search this whole searchspace. Perhaps a small group of boats cruise the lake, and some drones/helicopters fly the searchspace looking for the chipsat. And . . . we don't find it. Given our prior knowledge of the likelihood for the chipsat's location, and given our knowledge of the searchability for each region of the searchspace, we can update our knowledge of where the chipsat must be located.
\begin{align} &p(\text{chipsat is located in gridcell }|\text{ we did not find it}) =\\ &\frac{p(\text{chipsat is located in that cell}) \cdot p(\text{not finding the chipsat }|\text{ it is located in that gridcell})}{p(\text{not finding the chipsat})} \end{align}Note that this update does not require that we've searched the whole space. Everytime we search a single grid-cell, we can update this picture.
We can notice a few things which match our intuition. Given that we searched the whole lake, and given that the searchability of the lake is better than that of the land, we've decreased our confidence that the chipsat is in the lake (we'd probably have seen it). We've decreased our confidence that the chipsat is on the shore of the lake to an even greater degree, and we've increased our confidence that it's somewhere on the land. On land, it's more likely that we may have missed it in our search.
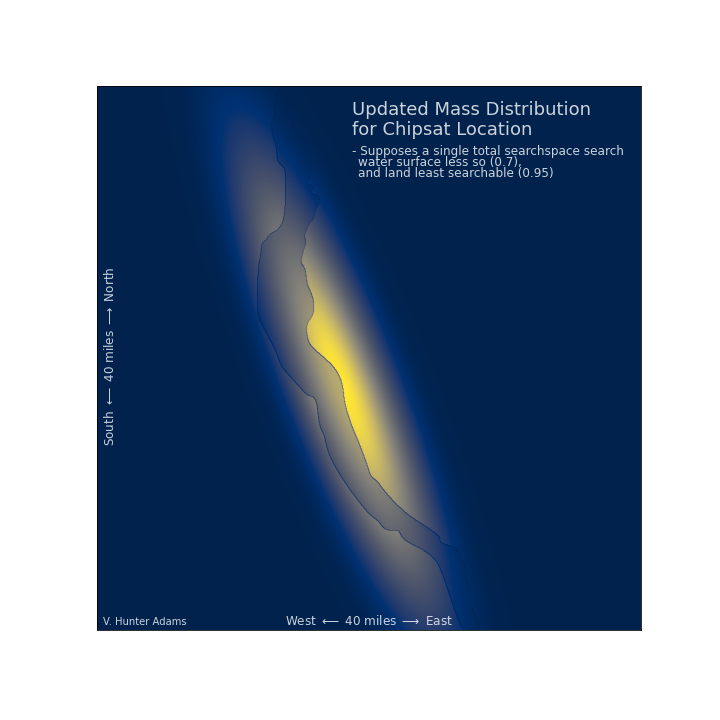
$\frac{p(\text{chipsat is located in that cell}) \cdot p(\text{not finding the chipsat }|\text{ it is located in that gridcell})}{p(\text{not finding the chipsat})}$
A north wind blows¶
Let us now suppose that a strong north wind blows overnight. We can incorporate this new information about the chipsat location into our infrastructure, to better inform the next day's search. As you can see, the north wind pushes any probability mass on the surface of the lake south, until it encounters a shore. The probability mass then accumulates on the shore. So, on the next day, it would be a wise decision to revisit the north-facing beaches of the lake, even though we've already searched them.
This should match intuition, but the point here is that such intuition emerges from this model. The Bayesian search formulation allows for us to make a best-guess about the chipsat's location that incorporates our prior knowledge about the situation, the searchability of the landing zone, the results of searches already conducted, and time-varying information about the probability distribution in the search space.
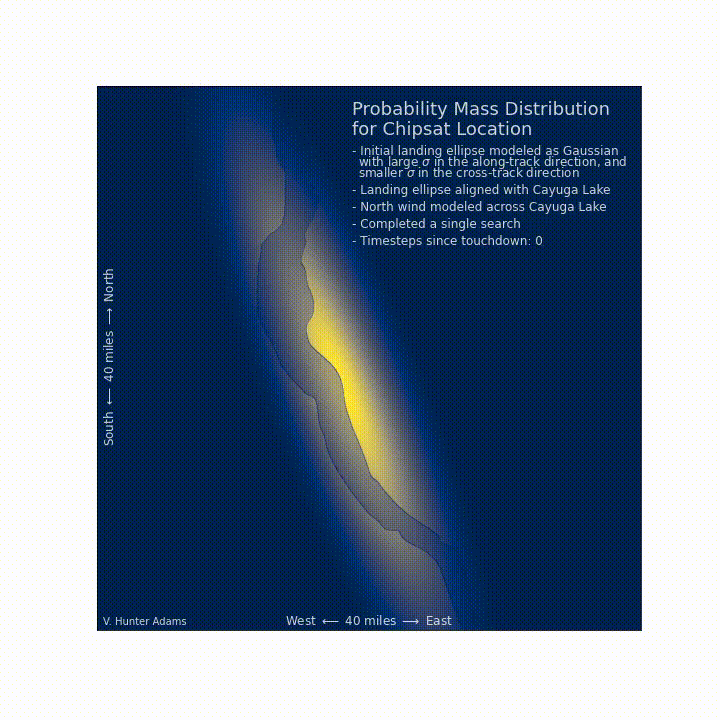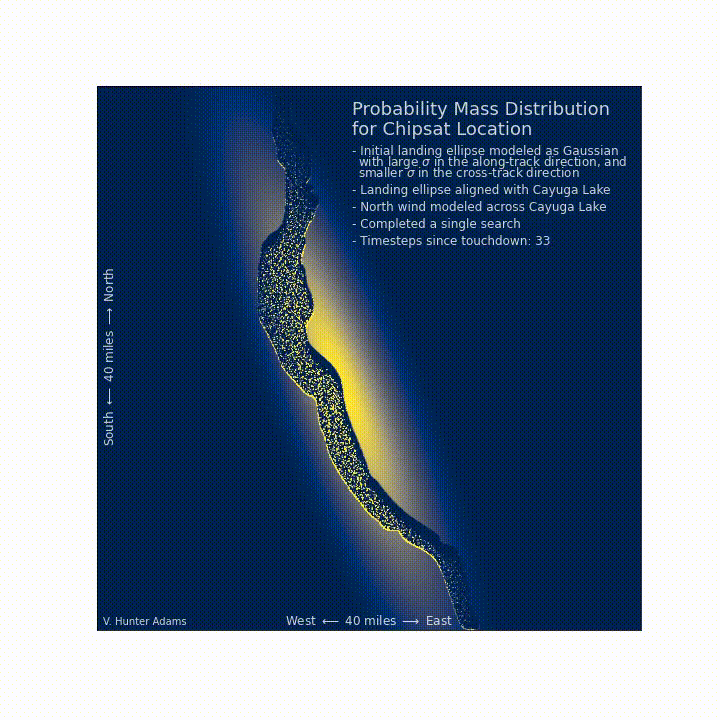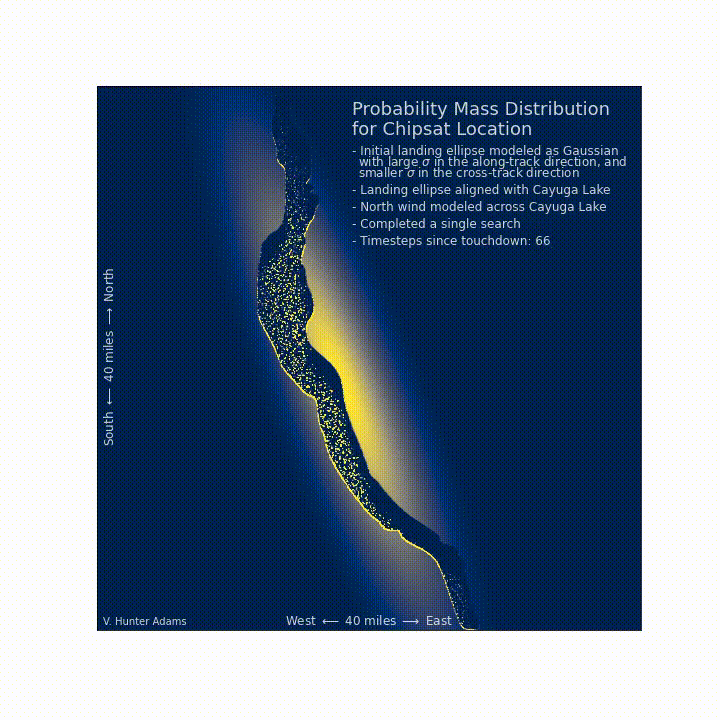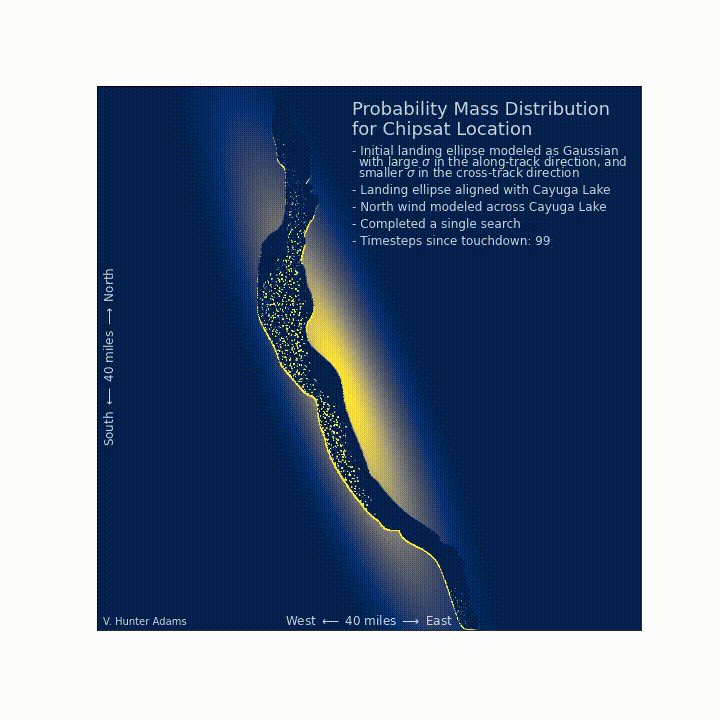
Updating our prioritized search¶
After having completed one comprehensive search, and after having a north wind blow across the lake, where should we prioritize our search the following day? We discover that we would be wise to revisit the north-facing shores of the lake.

$p(\text{chipsat is in gridcell})\cdot p(\text{finding chipsat in that gridcell})$
Generalizing to Dyson spheres¶
Let us now revisit each of the above steps, and discuss what this step looks like when applied to the search for Dyson spheres, rather than the search for a chipsat.
Where we begin for Dyson spheres¶
In the search for chipsats, we began with a totally uniform distribution across the searchspace. In the search for Dyson spheres, we have the same uniform probability distribution over a much larger searchspace. At the very beginning of this process, we've no reason to prefer any one location over another as a potential home for a Dyson sphere.
Incorporating expert knowledge to inform location probabilities for Dyson spheres¶
The next step in the search for chipsats was to use expert knowledge to develop a set of prior probabilities for each location in our searchspace. For the chipsats, this expert opinion came from knowledge of orbital mechanics, aerodynamics, the weather, etc. In the search for Dyson spheres, this expert opinion comes from a tremendously diverse group of individuals, like those at the Dyson Minds workshop. This group will attempt to agree upon the set of prior probabilities for Dyson Spheres existing in each stellar system in the galaxy, at each black hole in the galaxy, etc.
You could imagine organizing a workshop devoted to this effort. Such a workshop would begin with a uniform probability distribution across the galaxy for the existence of Dyson spheres. We would attempt to conclude the workshop with a picture of the updated probability distribution, which incorporates domain expertise to adjust this uniform prior up and down across the galaxy. We wouldn't yet worry about observability, just existence.
For each grid in the searchspace:
\begin{align}
\text{Goal of workshop} = p(\text{Dyson sphere exists})
\end{align}
Incorporating expert knowledge on searchability for Dyson spheres¶
In the search for chipsats, the next step was to incorporate expert knowledge on the searchability of each zone in the searchspace. For the chipsats, this searchability relates to the accessibility and observability of the surface of the Earth in that area. One could imagine organizing a second workshop dedicated to this effort for Dyson spheres.
In the search for Dyson spheres, this discussion of searchability would start with the presupposition that a Dyson sphere does exist at a particular gridcell in our search space, and attempt to assign a probability to finding that Dyson sphere if we were to search there. This conversation would attempt to quantify both the probability of gathering the necessary data from that place in the galaxy, and the probability of seeing a Dyson sphere in the data if we were to gather it. It's the product of these two probabilities that quantifies observability for that grid-cell.
For each grid in the searchspace:
\begin{align}
\text{Goal of workshop} &= p(\text{Dyson sphere is observable | Dyson sphere exists})\\
\end{align}
where:
\begin{align}
p(\text{Dyson sphere is observable}) = p(\text{Gathering necessary data for that grid cell}) \cdot p(\text{Dyson sphere visible in that data})
\end{align}
Prioritizing search for Dyson spheres¶
As in the search for chipsats, we can compute the likelihood of finding a Dyson sphere at each location in our search space. This likelihood is given by:
\begin{align} p(\text{Finding DS}) &= p(\text{DS exists at that location}) \cdot p(\text{Observing DS in the data})\\ &= p(\text{DS exists at that location}) \cdot p(\text{Gathering necessary data}) \cdot p(\text{Seeing the DS in the data}) \end{align}
Note that this naturally directs our attention to places from which we've already gathered data!! The strategy of combing data that we've already gathered will emerge naturally from this framework!!
Updating our knowledge after a search for Dyson spheres¶
After having generated prior probabilities for Dyson sphere locations, and quantifying the searchability for each zone in the searchspace, we would then look for Dyson spheres. This will include combing data that we've already gathered, and it will include gathering more data. Every time we don't find a Dyson sphere, we update our map. Even as we fail to locate these objects, we systematically narrow our search.
\begin{align} p(\text{DS is located in gridcell }|\text{ we did not find it}) = \frac{p(\text{DS is located in that cell}) \cdot p(\text{not finding the DS }|\text{ DS is located in that gridcell})}{p(\text{not finding the DS})} \end{align}A north wind blows for Dyson spheres¶
The north wind in the chipsat problem represents a change in our understanding of the underlying probability distribution. In the case of the chipsats, this came from an outside force moving things around in our searchspace. In the case of the Dyson spheres, this may instead come from an improved understanding of our searchspace. That is, everytime we learn anything about our galaxy/universe that is of relevance to the search for Dyson spheres, this model allows for us to immediately incorporate that information into our search. Our map will update at the same rate relevant scientific publications appear. We narrow our search even when we aren't actively looking, simply by paying attention to growing knowledge of relevance.
Put alternatively, a workshop dedicated to this question would discuss how the observability of a Dyson sphere may change as a function of other things happening in the universe. Does Betelguese going nova increase observability of the cells around that star? Does a collision with some object that may induce Kessler syndrome temporarily increase observability? This would be a conversation in which we attempt to enumerate all the transient events which may make a Dyson sphere momentarily more observable in a particular location. It takes the heatmap from the first workshop and makes it a function of time..
For each grid in the searchspace:
\begin{align}
\text{Goal of workshop} = p(\text{Dyson sphere exists}) = f(t)
\end{align}
Updating our prioritized search for Dyson spheres¶
As with the chipsats, we can recompute the likelihood of finding the Dyson sphere at each possible location in our searchspace, given our updated likelihood distribution for the Dyson sphere existing at each possible location, the probability of gathering the necessary data to see it, and the probability of seeing it in that data.
Some thoughts on prior probabilities¶
It seems to me that one of the first steps in establishing reasonable guesses for the prior probabilities of Dyson spheres existing throughout our searchspace is to elaborate a taxonomy of the various types of Dyson spheres. Some of these will be the product of deliberate engineering, others will be the organic product of evolution, and some may fit somewhere inbetween. Some may be coherent minds and others may be societies of mind. We may then arrive at a total probability of Dyson sphere existence by summing the probabilities for each species, or perhaps instead we maintain probability maps for each species separately.
I think careful thought about this taxonomy is helpful, because each species of Dyson sphere may have its own set of motivations. For an entity like a Dyson mind, motivation couples closely with observability.
I think we should seriously consider the possiblity that Dyson Minds are camouflaging themselves as nature. A sufficiently advanced computer may be indistinguishable from nature, and perhaps the fact that we haven't already found an engineered Dyson sphere means that they are masquerading as normal stars, black holes, etc.
Some thoughts on searchability¶
Under normal conditions¶
- In the taxonomic tree of Dyson spheres, an early branch separates those which are the product of engineering from those which are the product of evolution.
- An engineered system looks different from nature under normal conditions, and evolved one may only look different under special conditions. But perhaps that makes it more observable.
- There are three reasons that an evolved Dyson sphere may not be observable under normal conditions.
- If a sufficiently advanced computer is indistinguishable from nature, then we may be unable to discern an intelligent entity from inanimate stars, black holes, galaxies, etc. If computers converge upon a natural-looking design, then it may be hard to look for the “pieces” of the computer. Like our brains, everything is all mixed up everyplace.
- Furthermore, it may be the case that such an entity has a desire to camouflage itself, which means it would try to look natural.
- And finally, the rate of cognition for a Dyson sphere is probably so slow that we’d never observe a conscious action. If there existed an intelligence that survived a millisecond or a microsecond, what would it observe about us in order to conclude that we are intelligent entities?
- If we wanted to look for an evolved Dyson sphere operating under normal conditions, I would be inclined to look for places where free will can be disguised as a natural process. Perhaps chaotic systems?
Under special conditions¶
- But perhaps such a Dyson sphere is more “findable” because we can make educated guesses about the circumstances under which it would abandon its camouflage. I think these circumstances include:
- Self-preserving reflex responses taken in response to existential threads. Kessler syndrome, supernovae, etc. These are things which happen over human timescales that may require self-preserving response by the Dyson sphere. The analog to a hunting dog flushing camouflaged birds. Might we observe them mitigating or fleeing these risks?
- An end-of-life cry to the universe “I existed.” Can a society-of-mind Dyson Mind become unstable? Perhaps Betelgeuse is an intelligent entity, disguised as a natural system, losing control. When it goes nova, it may abandon all attempt at camouflage and put information about itself into the nova. When that happens, I think we should look for it.
Observability of information transport¶
- In our own bodies, some of our mechanisms for information transport are rather slow because they’re chemically mediated. We haven’t evolved to minimize latency. Maybe the Dyson sphere hasn’t either.
- Maybe the Dyson sphere evolved to maximize bandwidth, even at the cost of latency. This might imply that information is being transported via matter, and maybe that’s something we could look for
- Could we look for stuff streaming from place to place, rogue planets and the like?
- Is it conceivable that dark matter is their medium for communication? This would certainly keep them camouflaged.
- Well compressed data (with all redundancies removed) looks like noise. Maybe this makes it harder to discover messages encoded in matter, or maybe it makes it easer? Could we somehow measure the amount of redundant information in the state of interstellar matter? Is there anywhere in nature that’s too random?
- Could we observe this matter being read or written?
- Perhaps there are some events that require low-latency communication in advance of higher-latency and higher-bandwidth communication? An impending collision? Colliding galaxies may be places to look for communication between Dyson spheres.
Observability of information storage¶
- Would a Dyson mind want to record its history? Where are the most information dense, non-volatile places in the universe? Could we search these places to see if the information stored there is suspiciously lacking in redundancy?
Historical precedent for Bayesian search¶
Though I'm not aware of these techniques being applied to the search for Dyson spheres (please correct me if I'm wrong!!), they have been applied a number of other high-stakes search situations. Many of these are described in a lovely book by Shannon McGrayne called The Theory That Would Not Die. Some interesting examples include:
- The 1966 Palomares incident: An H-Bomb was lost in the Mediterranean Sea, they found it by means of a Bayesian search in 80 days.
- Finding the USS Scorpion): In May 1968, a nuclear-powered attack sub disappeared in the Atlantic, Bayes found it.
This technique is a standard part of the Coast Guard's search protocol.