Boids algorithm - augmented to include a predator

V. Hunter Adams

• Background and Introduction
• Algorithm Overview

  • Separation
  • Alignment
  • Cohesion
  • Screen edges
  • Predator avoidance
  • Speed limits
  • Update position
  • Recommended parameter values
  • Pseudocode

Background and Introduction

Boids is an artificial life program that produces startlingly realistic simulations of flocking behavior. Each "boid" (which is an abbreviation of "bird-oid object" follows a very simple set of rules. These rules will be discussed at length, but they can be summarized as follows:

• Separation: boids move away from other boids that are too close
• Alignment: boids attempt to match the velocities of their neighbors
• Cohesion: boids move toward the center of mass of their neighbors

We will add a few more rules to this list. In particular, boids will turn around at the boundaries of the VGA display, their speeds will be constrained to within a configurable range, and we will have the boids avoid a predator.

When all of the boids follow these simple rules, the flock produces gorgeously organic-looking emergent patterns, as shown in the video below. You can compare the simulated behavior to videos of actual murmurations of starlings (like this one). The Boids algorithm was developed by Craig Reynolds in 1986.

Algorithm Overview

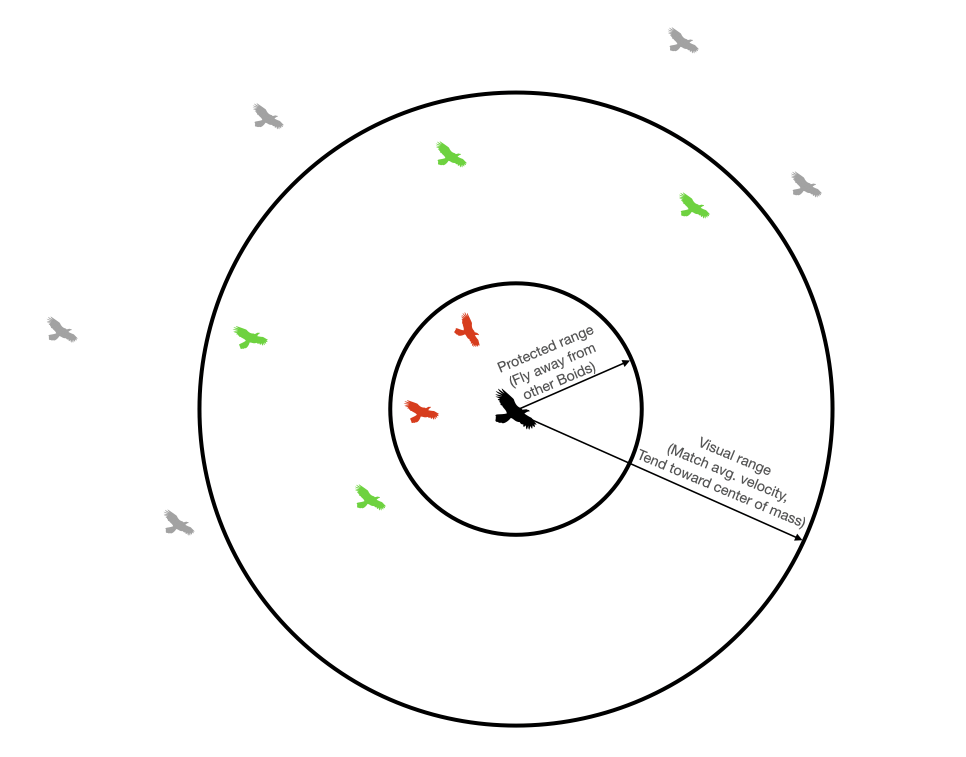
Just like in nature, no boid has global knowledge of every other boid in the flock. Instead, each can only see boids that are within its visual range and that are within its smaller protected range. These are tunable parameters. A boid will move away from other boids that are within its protected range (birds don't want to fly into each other), it will attempt to match the average velocity of boids within its visible range, and it will tend toward the center of mass of boids in its visible range.

We will also enforce minimum and maximum speed limits for the boids. Flocking birds (like starlings) are never stationary in flight. So, we'll prevent the speed of any boid from dropping below some tunable value. Birds also have maximum speeeds, so we'll prevent the speed of any boid from exceeding some tunable value. Finally, we want for the boids to turn around when they reach the edges of the VGA screen. When a boid gets within some tunable margin of an edge of the screen, we will turn it by some tunable value. The greater this value, the faster the birds will be able to turn. We can play with these parameters until we get realistic-looking behavior.

The state for each boid includes its x/y position and its x/y velocity, represented as:
boid.x
boid.y
boid.vx
boid.vy

Each boid determines whether each other boid is in its protected/visual range.

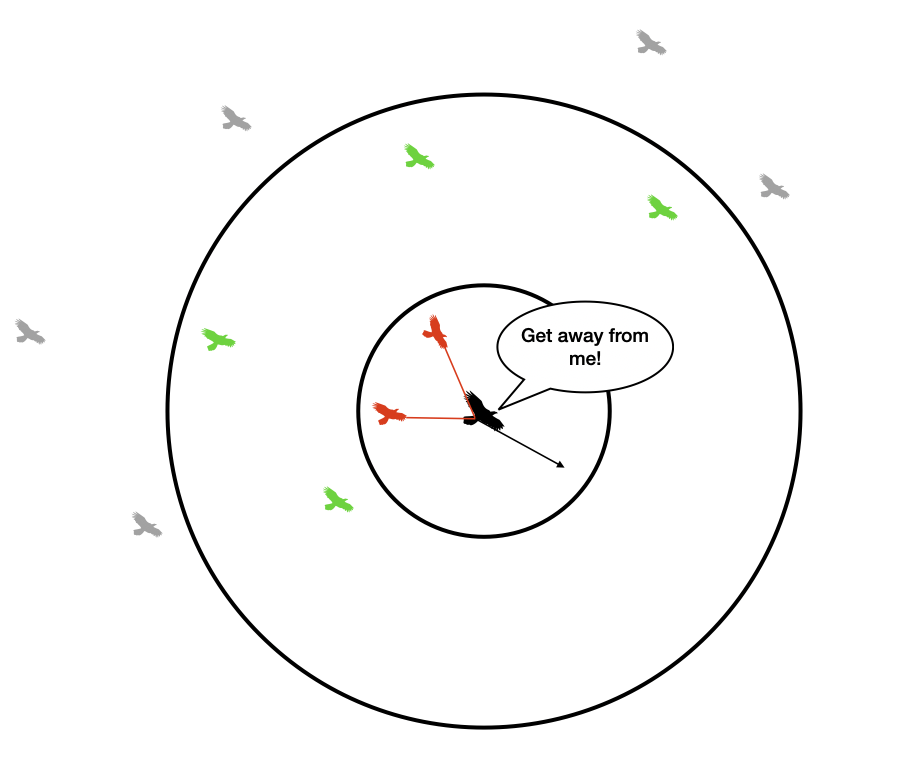
Separation

Each boid attempts to avoid running into other boids. If two or more boids get too close to one another (i.e. within one another's protected range), they will steer away from one another. They will do so in the following way:

1. At the start of the update for a particular boid, two accumulating variable (close_dx and close_dy) are zeroed
2. We loop thru every other boid. If the distance to a particular boid is less than the protected range, then
   close_dx += boid.x - otherboid.x
close_dy += boid.y - otherboid.y.
3. Once we've looped through all other boids, then we update the velocity according to
   boid.vx += close_dx*avoidfactor
boid.vy += close_dy*avoidfactor
   (where avoidfactor is a tunable parameter)

Move away from boids in protected range.

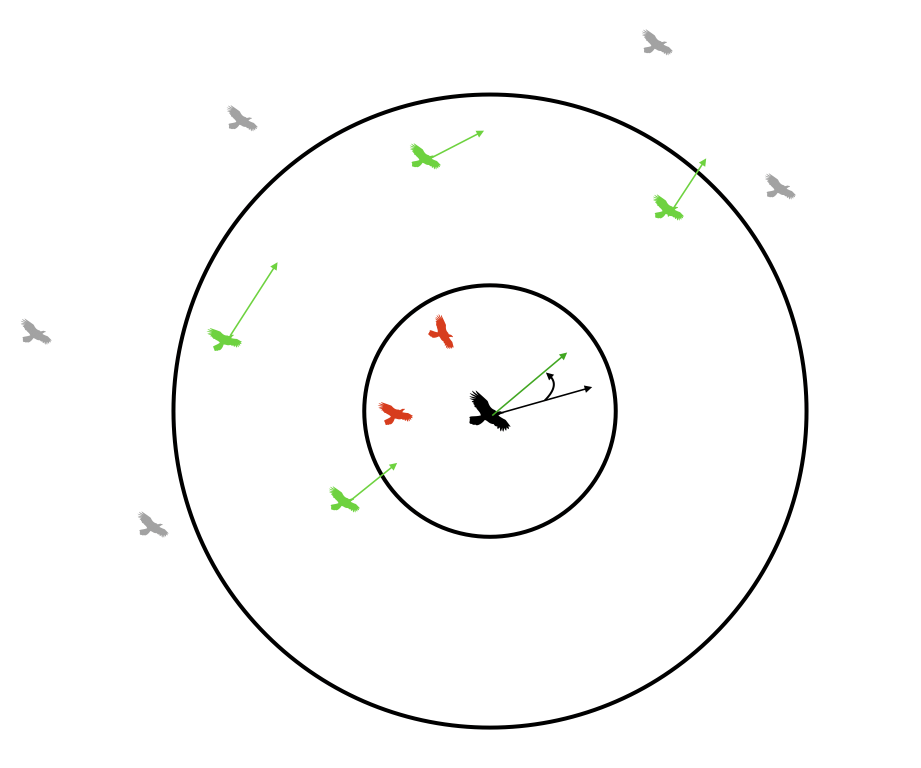
Alignment

Each boid attempts to match the velocity of other boids inside its visible range. It does so in the following way:

1. At the start of the update for a particular boid, three variables (xvel_avg, yvel_avg, and neighboring_boids) are zeroed
2. We loop thru every other boid. If the distance to a particular boid is less than the visible range, then
   xvel_avg += otherboid.vx
yvel_avg += otherboid.vy
neighboring_boids += 1
3. Once we've looped through all other boids, we do the following if neighboring_boids>0:
   xvel_avg = xvel_avg/neighboring_boids
yvel_avg = yvel_avg/neighboring_boids
4. We then update the velocity according to:
   boid.vx += (xvel_avg - boid.vx)*matchingfactor
boid.vy += (yvel_avg - boid.vy)*matchingfactor
   (where matchingfactor is a tunable parameter)

Align with average velocity of boids in visible range.

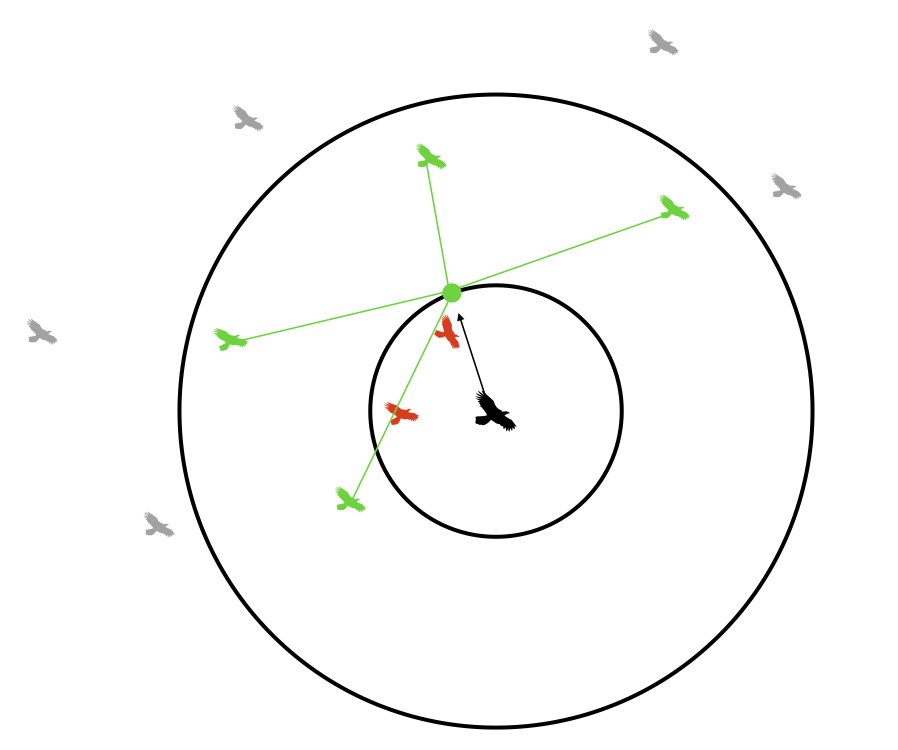
Cohesion

Each boid steers gently toward the center of mass of other boids within its visible range. It does so in the following way:

1. At the start of the update for a particular boid, three variables (xpos_avg, ypos_avg, and neighboring_boids) are zeroed
2. We loop thru every other boid. If the distance to a particular boid is less than the visible range, then
   xpos_avg += otherboid.x
ypos_avg += otherboid.y
neighboring_boids += 1
3. Once we've looped through all other boids, we do the following if neighboring_boids>0:
   xpos_avg = xpos_avg/neighboring_boids
ypos_avg = ypos_avg/neighboring_boids
4. We then update the velocity according to:
   boid.vx += (xpos_avg - boid.x)*centeringfactor
boid.vy += (ypos_avg - boid.y)*centeringfactor
   (where centeringfactor is a tunable parameter)

Move toward center of mass of boids in visible range.

Screen edges

We want our boids to turn-around at an organic-looking turn radius when they approach an edge of the TFT. We will do so in the following way:

if boid.x < leftmargin:
    boid.vx = boid.vx + turnfactor
if boid.x > rightmargin:
    boid.vx = boid.vx - turnfactor
if boid.y > bottommargin:
    boid.vy = boid.vy - turnfactor
if boid.y < topmargin:
    boid.vy = boid.vy + turnfactor

where turnfactor and all margins are tunable parameters. I recommend a margin of 100 pixels on all edges.

Steer away from edges of VGA display.

Predator

ECE 5730 students are required to add a predator to the simulation. This predator moves like any other Boid, except that its only velocity updates come from turning at the screen edges (it does not perform any separation, cohesion, or alignment calculations).

The Boids, of course, avoid the predator. They do so in the following way:

1. For each Boid compute the distance from the Boid to the predator in each dimension:
   predator_dx = boid.x - predator.x
predator_dy = boid.y - predator.y
   
2. If the distance to the predator is less than the predatory range (a tunable parameter), then turn away from the predator:
   

   if (predator_dy > 0) { //predator above boid
   boid.vy = (boid.vy + predatorturnfactor) ;
   }
   if (predator_dy < 0) { //predator below boid
   boid.vy = (boid.vy - predatorturnfactor) ;
   }
   if (predator_dx > 0) { //predator left of boid
   boid.vx = (boid.vx + predatorturnfactor) ;
   }
   if (predator_dx < 0) { //predator right of boid
   boid.vx = (boid.vx - predatorturnfactor) ;
   }
   

   where predatorturnfactor, similarly to turnfactor, dictates how sharply a boid is capable of turning away from a predator.

Speed limits

We constrain the boids to move faster than some minimum speed and slower than some maximum speed. We do so in the following way:

1. Once the velocity has been updated, compute the boid speed
   speed = sqrt(boid.vx*boid.vx + boid.vy*boid.vy)
2. If speed>maxspeed:
   boid.vx = (boid.vx/speed)*maxspeed
boid.vy = (boid.vy/speed)*minspeed
3. If speed<minspeed:
   boid.vx = (boid.vx/speed)*minspeed
boid.vy = (boid.vy/speed)*minspeed

Update position

With the updated velocity, we update the boid position. Assume that $\Delta t = 1$ from frame to frame (i.e. that velocity is in units of pixels/frame):

boid.x = boid.x + boid.vx
boid.y = boid.y + boid.vy

Recommended parameter values

You can play with these to get different emergent behaviors. These are the parameters that I used in the example videos on this webpage. Note that you will need to convert these to fixed-point.

turnfactor: 0.2
visualRange: 40
protectedRange: 8
centeringfactor: 0.0005
avoidfactor: 0.05
matchingfactor: 0.05
maxspeed: 6
minspeed: 3
predatorturnfactor: 0.5
predatorRange: 100

Pseudocode

All of the above rules are represented in the below pseudocode. Look for places to optimize! This pseudocode describes the most straightforward implementation of the algorithm, there are lots of opportunities to speed things up.

# For every boid . . .
for each boid (boid):

    # Zero all accumulator variables (can't do this in one line in C)
    xpos_avg, ypos_avg, xvel_avg, yvel_avg, neighboring_boids, close_dx, close_dy = 0

    # For every other boid in the flock . . .
    for each other boid (otherboid):

        # Compute differences in x and y coordinates
        dx = boid.x - otherboid.x
        dy = boid.y - otherboid.y

        # Are both those differences less than the visual range?
        if (abs(dx)<visual_range and abs(dy)<visual_range):  

            # If so, calculate the squared distance
            squared_distance = dx*dx + dy*dy

            # Is squared distance less than the protected range?
            if (squared_distance < protected_range_squared):

                # If so, calculate difference in x/y-coordinates to nearfield boid
                close_dx += boid.x - otherboid.x 
                close_dy += boid.y - otherboid.y

            # If not in protected range, is the boid in the visual range?
            else if (squared_distance < visual_range_squared):

                # Add other boid's x/y-coord and x/y vel to accumulator variables
                xpos_avg += otherboid.x 
                ypos_avg += otherboid.y 
                xvel_avg += otherboid.vx
                yvel_avg += otherboid.vy

                # Increment number of boids within visual range
                neighboring_boids += 1 


    # If there were any boids in the visual range . . .            
    if (neighboring_boids > 0): 

        # Divide accumulator variables by number of boids in visual range
        xpos_avg = xpos_avg/neighboring_boids 
        ypos_avg = ypos_avg/neighboring_boids
        xvel_avg = xvel_avg/neighboring_boids
        yvel_avg = yvel_avg/neighboring_boids

        # Add the centering/matching contributions to velocity
        boid.vx = (boid.vx + 
                   (xpos_avg - boid.x)*centering_factor + 
                   (xvel_avg - boid.vx)*matching_factor)

        boid.vy = (boid.vy + 
                   (ypos_avg - boid.y)*centering_factor + 
                   (yvel_avg - boid.vy)*matching_factor)

    # Add the avoidance contribution to velocity
    boid.vx = boid.vx + (close_dx*avoidfactor)
    boid.vy = boid.vy + (close_dy*avoidfactor)


    # If the boid is near an edge, make it turn by turnfactor
    # (this describes a box, will vary based on boundary conditions)
    if outside top margin:
        boid.vy = boid.vy + turnfactor
    if outside right margin:
        boid.vx = boid.vx - turnfactor
    if outside left margin:
        boid.vx = boid.vx + turnfactor
    if outside bottom margin:
        boid.vy = boid.vy - turnfactor

    ####################################################################################
    ######################### 5730 students only #######################################
    ####################################################################################
    # For every predator . . .
    for each predator (predator):

        # Compute the differences in x and y coordinates
        dx = boid.x - predator.x
        dy = boid.y - predator.y

        # Are both those differences less than the predatory range?
        if (abs(dx)<predatory_range and abs(dy)<predatory_range):

            # If so, calculate the squared distance to the predator
            squared_predator_distance = dx*dx + dy*dy

            # Is the squared distance less than the predatory range squared?
            if (squared_predator_distance < predatory_range_squared):

                # If so, accumulate the differences in x/y coordinates to the predator
                predator_dx += boid.x - predator.x
                predator_dy += boid.y - predator.y

                # Increment the number of predators in the boid's predatory range
                num_predators += 1

    # If there were any predators in the predatory range, turn away!
    if (num_predators > 0):
        if predator_dy > 0:
            boid.vy = boid.vy + predator_turnfactor
        if predator_dy < 0:
            boid.vy = boid.vy - predator_turnfactor
        if predator_dx > 0:
            boid.vx = boid.vx + predator_turnfactor
        if predator_dx < 0:
            boid.vx = boid.vx - predator_turnfactor     
    ####################################################################################


    # Calculate the boid's speed
    # Slow step! Lookup the "alpha max plus beta min" algorithm
    speed = sqrt(boid.vx*boid.vx + boid.vy*boid.vy)

    # Enforce min and max speeds
    if speed < minspeed:
        boid.vx = (boid.vx/speed)*minspeed
        boid.vy = (boid.vy/speed)*minspeed
    if speed > maxspeed:
        boid.vx = (boid.vx/speed)*maxspeed
        boid.vy = (boid.vy/speed)*maxspeed

    # Update boid's position
    boid.x = boid.x + boid.vx
    boid.y = boid.y + boid.vy

---

---