Digital Galton Board¶

V. Hunter Adams ¶

Introduction¶

In this laboratory exercise, you will engineer a digital version of a Galton Board, which is one of the most famous physical demonstrations of order from chaos that has ever been constructed. The Galton Board delightfully combines five famous mathematical concepts: Bernoilli trials, the binomial distribution, the Gaussian distribution, Pascal's triangle, and the central limit theorem.

A Galton Board is composed of interleaved rows of pegs. When one drops a ball onto the top row of pegs, it bounces its way to the bottom and ultimately lands in one of N+1 bins that rest between and beneath the N lowest pegs in the board. In an idealized Galton Board, the ball bounces against a peg in each row of the board. When it strikes that peg, it has a 50% chance of bouncing to the left, and a 50% chance of bouncing to the right. If you repeat this experiment over and over and over again, the count of balls in the bins forms a nice clean binomial distribution. And as the number of rows increases and the number of trials increases, this binomial distribution, by the central limit theorem, approaches a Gaussian distribution.

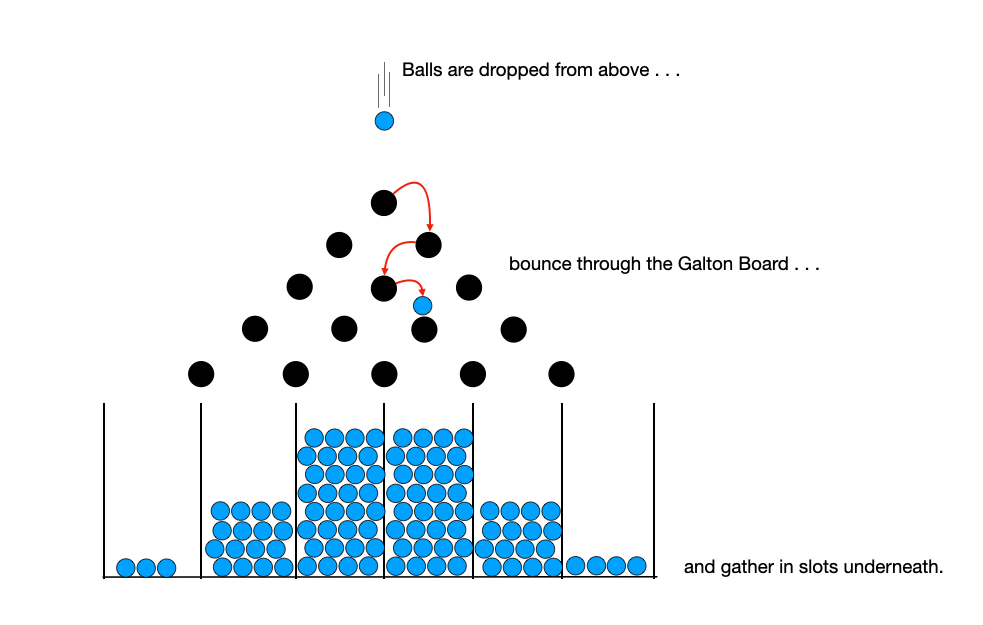
It is really startling to watch! In fact, this phenomenon so impressed Francis Galton that he stated:

The law [the central limit theorem] would have been personified by the Greeks and deified, if they had known of it. It reigns with serenity and in complete self-effacement amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason. Whenever a large sample of chaotic elements are taken in hand and marshalled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along.

You will build a digital version of a board, through which you will drop as many balls as you can manage at 30 frames per second. The more thoughtful and efficient your code, the more balls you will be able to animate. Every time any ball strikes a peg there must be a "thunk!" sound effect. You don't want to waste cycles doing interrupt-based audio synthesis, so you will use a DMA channel to trigger the sound effects. The balls will bounce according to collision physics. You must count and plot the number of balls that land in each bin at the bottom of the board so that we can see the central limit theorem in action. You will implement a potentiometer-based interface that allows for the user to adjust parameters in realtime and thereby "play" with the central limit theorem.

Key concepts: Fixed point arithmetic, optimization, direct memory access, SPI, collision physics, analog to digital converter, computer animation, VGA, PIO, alpha max beta min, overclocking, multicore parallelism, binomial distribution, Gaussian distribution, central limit theorem, Pascal's triangle.

Demonstration¶

Reading¶

Experience shows that students prefer these webpages short. For that reason, plese find the reading and background materials on the webpages linked below. Please note that the information in these readings will be critical for completing the lab.

Math and physics background

The statistics of an idealized Galton Board: Bernoilli, Binomial, and Gaussian, oh my!
The physics of colliding balls, with coefficient of restitution: Describes the physics that you will be implementing.
Alpha max plus beta min algorithm: An efficient algorithm for computing quick-and-dirty root sum of squares.

Engineering background

VGA driver: You will not be asked to implement a VGA driver, you will use the one described on this webpage. You will need to modify it if you want to overclock the RP2040.
Fixed-point arithmetic: To animate the most-possible balls, you want for your arithmetic to be as fast as possible. Floating point is too slow. Fixed-point arithmetic allows for you to use integer arithmetic (which is way faster than floating point, on this architecture) while maintaining fractional resolution.
SPI interface: You will generate sound effects by means of an SPI DAC. An understanding of this interface will help you debug.
DAC datasheet: Datasheet for the MCP4822 DAC we'll be using in this lab.
RP2040 datasheet: Sections on DMA, UART, Multicore, Timers, PIO, ADC, GPIO
RP2040 C SDK guide: Same sections as above

Some collision-physics pseudocode

Some pseudocode that shows how ball positions are updated each frame:

// Pseudocode for updating a ball's position between frames.
// There are LOTS of opportunities to optimize this! Look for ways
// to speed this up!!

// Each frame, we update every ball . . .
for each ball:

    // Every ball looks at every peg . . .
    for each peg:

        // Compute x and y distances between ball and peg
        dx = ball.x - peg.x
        dy = ball.y - peg.y

        // Are both the x and y distances less than the collision distance?
        if ((|dx| < (ball.radius + peg.radius)) and (|dy| < (ball.radius + peg.radius))):

            // If so, compute the distance separating ball and peg
            distance = sqrt(dx^2 + dy^2)

            // Generate the normal vector that points from peg to ball
            normal_x = dx/distance
            normal_y = dy/distance

            // Collision physics (see webpage)
            intermediate_term = -2*((normal_x * ball.vx) + (normal_y * ball.vy))

            // Are the ball velocity and normal vectors in opposite directions?
            if (intermediate_term > 0):

                // Teleport it outside the collision distance with the peg
                ball.x = peg.x + (normal_x * (distance+1))
                ball.y = peg.y + (normal_y * (distance+1))

                // Update its velocity (see collision physics webpage)
                ball.vx = ball.vx + (normal_x * intermediate_term)
                ball.vy = ball.vy + (normal_y * intermediate_term)

                // Did we just strike a new peg?
                if current_peg != last_peg:

                    // Make a sound
                    dma.trigger()

                    // Remove some energy from the ball
                    ball.vx = bounciness * ball.vx
                    ball.vy = bounciness * ball.vy

    // Re-spawn any balls that fall thru bottom
    if hit bottom:
        re-spawn at top

    // Bounce any balls that hit top/sides
    if hit left/right/top:
        invert appropriate velocity component to bounce


    // Apply gravity
    ball.vy = ball.vy + gravity

    // Use ball's updated velocity to update its position
    ball.x = ball.x + ball.vx
    ball.y = ball.y + ball.vy

Weekly Checkpoints¶

Note that these checkpoints are cumulative. In week 2, for example, you must have also completed all of the requirements from week 1.

Week 1

Starting from this example, and using the pseudocode above (which comes from the collision physics for the digital Galton Board webpage), get one ball to bounce off one peg.
- This ball should be "dropped" from the top of the screen with zero y-velocity, and a randomized (small) x-velocity.
- The ball should accelerate downward by gravity and collide with the peg underneath, bouncing off.
- There should be an audible sound effect, generated by DMA, when the ball strikes the peg. Modify the DMA channels from this example to generate the sound effect.
- When the ball exits the bottom of the screen, it should automatically drop again from the top.
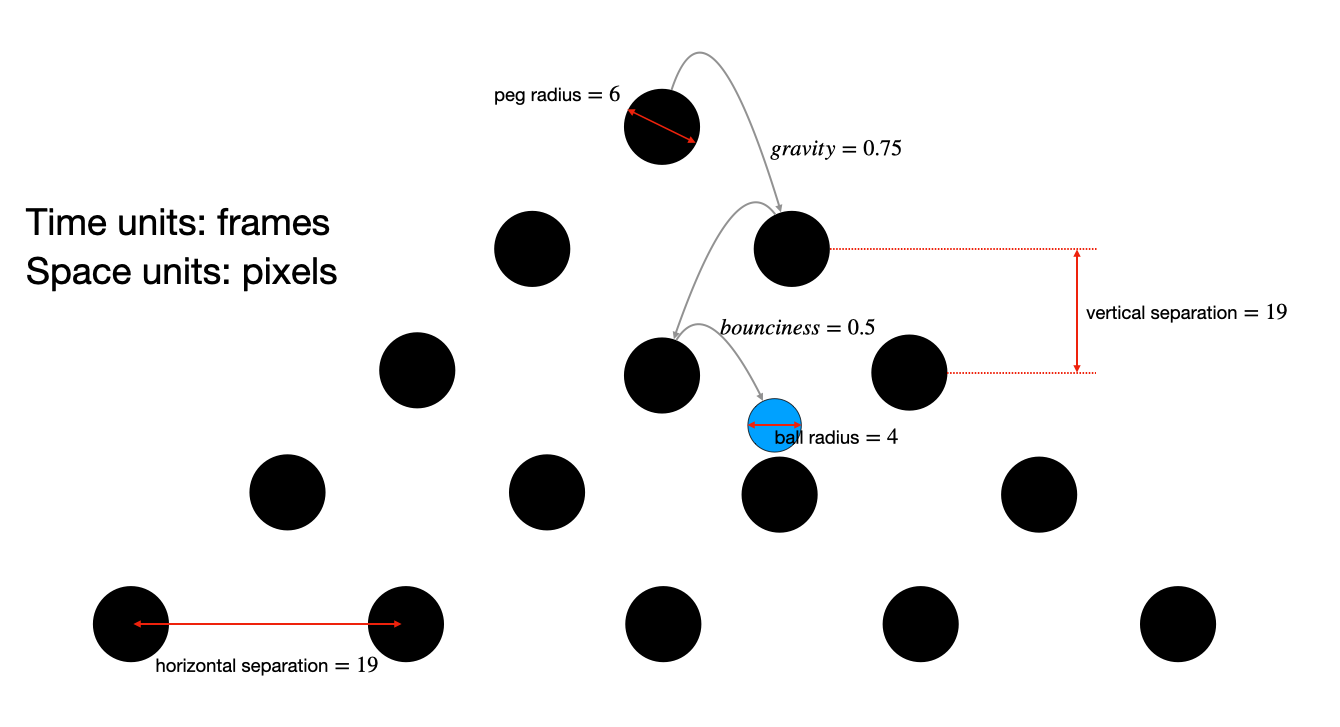
- Use the default parameters provided in the image below.

Week 2

Generate the 16-row Galton Board, and animate at least 10 balls falling through it. Each ball should generate a sound effect when it collides with a new peg, and each should be re-spawned when it falls thru the bottom of the screen.
The user should be able to adjust the number of balls by means of a potentiometer.
The VGA screen should display:
- The current number of balls being animated.
- The total number that have fallen through the board since reset.
- Time since boot
Generate a histogram underneath the Galton Board that shows the number of balls that have fallen through each pair of pegs in the bottom row.
Normalize the height of the histogram to the available vertical space beneath the Galton Board.

Week 3

At reset, the maximum number of balls which you can animate at 30fps should be dropped into the top of the Galton Board.
Each of these balls should generate a "thunk" sound when it hits a new peg.
The user interface is an external button and a potentiometer. At reset, the potentiometer should not affect the animation. Upon a button push, the potentiometer adjusts the number of balls. Upon a second push, the potentiometer adjusts the bounciness parameter. The user should be able to cycle through all these states via repeated button pushes, and the state should be shown on the VGA display.
A histogram, normalized to the available vertical space beneath the Galton Board, should show the number of balls that have fallen through each pair of pegs in the bottom row.
The VGA screen should display:
- The current number of balls being animated.
- The total number that have fallen through the board since reset.
- Values of other tunable parameters
- Time since boot
Adjusting any parameter by means of the potentiometer should reset the histogram, and reset the total number of balls that have fallen through the board since reset.
If the 30fps deadline is missed, the LED should turn on.
5730 students only: Add another state, in which the potentiometer adjusts any one of the other Galton board parameters.

Lab Report¶

Your lab report should include all the sections mentioned on the policy page, and also answer the following questions:

Our physical model of the Galton Board differs from the idealized model. In order for the Central Limit Theorem to hold, all random numbers must be independent, identically distributed, and have finite variance. Which of these assumptions hold for our physical Galton Board model, and which do not? Why do we still see a distribution that approaches a Gaussian? (You needn't prove anything here, just try to identify the generalization of the CLT that is responsible for this).
The Gaussian approximates the distribution under the Galton board better with more rows in the board. Why?
For your 16-row Galton Board, what is the mean and standard deviation of the Gaussian which approximates the resulting distribution (under the assumption that your Galton Board is "ideal")?